
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема: однофакторный дисперсионный анализ
|
|
|
|
1o. Условия применимости метода
Дисперсионный анализ – статистический метод исследования влияния многоуровневых факторов на нормальную случайную величину Х генеральной совокупности по значениям межгрупповых дисперсий выборочных данных.
Следует отметить, что при дисперсионном анализе уровни фактора могут быть как градациями количественных характеристик воздействия фактора (например, уровни финансирования, уровни спроса, степень государственного участия в бизнесе и т.п.), так и градациями качественных характеристик (например, формы управления в частном секторе бизнеса, различные подходы к внедрению инновационных технологий, последовательность мероприятий при управлении кадровой политикой на предприятии, цвет стимулирующего фактора и т.п.).
Основные условия применимости дисперсионного анализа:
1) факторы должны быть многоуровневыми, т.е. выборочные данные можно расчленить на группы, каждая из которых соответствует определенному уровню того или иного фактора;
2) факторы должны быть независимыми, а их влияние на случайную величину Х полагается аддитивным;
3) распределение выборочных данных в каждой группе должно быть нормальным;
4) несмещенная оценка дисперсии случайной величины Х должна быть одинаковой для всех групп.
Примечание. Если объем выборки на всех уровнях для каждого фактора одинаковый, то небольшие отклонения от условий 3) и 4) на результате анализа не отражаются. Однако, если соответствующие объемы выборки различны, то результат анализа может оказаться весьма чувствительным к таким отклонениям.
Рассмотрим модель однофакторного дисперсионного метода, в которой выборки на каждом уровне воздействующего фактора независимы.
Ограничения использования метода для рассматриваемой модели:
Ø уровней (градаций) действия фактора должно быть не менее трех;
Ø объем выборки на каждом уровне действия фактора должен быть не менее двух;
Ø должно выполняться равенство дисперсий всех генеральных совокупностей, к которым принадлежат полученные независимые выборки по всем уровням действия фактора;
В однофакторном дисперсионном анализе принимается одна из гипотез: основная Н 0: различие признака на разных уровнях воздействующего фактора является не более выраженным, чем случайные различия этого признака внутри каждого уровня; альтернативная Н 1: различие признака на разных уровнях воздействующего фактора является более выраженным, чем случайные различия этого признака внутри каждого уровня.
2o. Математическая модель метода
В однофакторном дисперсионном анализе на случайную величину Х генеральной совокупности воздействует фактор А, который может действовать на т своих уровнях: А 1, А 2, …, Ап. Для каждого уровня делается выборка объемом п, т.е. выборочные данные можно представить матрицей размера т × п: 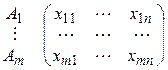 . В однофакторном дисперсионном анализе для выборочных значений признака xij принимается за основу линейная вероятностная схема: xij =
. В однофакторном дисперсионном анализе для выборочных значений признака xij принимается за основу линейная вероятностная схема: xij =  + a i + e ij, где xij – результат j -го наблюдения на i -м уровне фактора А,
+ a i + e ij, где xij – результат j -го наблюдения на i -м уровне фактора А,  – несмещенная оценка М (Х) = а, a i – эффект действия фактора А на i -м уровне, e ij – нормальная случайная величина с нулевым математическим ожиданием на каждом уровне, обусловленная влиянием неучтенных факторов и условий.
– несмещенная оценка М (Х) = а, a i – эффект действия фактора А на i -м уровне, e ij – нормальная случайная величина с нулевым математическим ожиданием на каждом уровне, обусловленная влиянием неучтенных факторов и условий.
Полагая, что выборка сделана из генеральной совокупности с нормально распределенной случайной величиной Х (т.е. Х ~ N (a; s), причем математическое ожидание М (Х) = а и стандартное отклонение s считаются неизвестными) и задавая уровень значимости a, проверяем основную гипотезу Н 0 о равенстве средних значений Х на всех уровнях действия фактора А, т.е. Н 0: а 1 = а 2 = … = ат = а; Н 1: не все ai одинаковы, 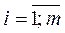 .
.
При выборе критерия для проверки гипотезы Н 0 следует учесть, что если Н 0 верна, т.е. все ai = а, то общее выборочное среднее  =
= 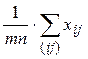 , где тп – объем объединенной выборки, не должен значительно отличаться от групповых средних
, где тп – объем объединенной выборки, не должен значительно отличаться от групповых средних 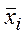 =
= 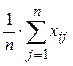 (суммирование выполняется по строке матрицы выборочных данных). Если же Н 0 не верна, то разброс
(суммирование выполняется по строке матрицы выборочных данных). Если же Н 0 не верна, то разброс 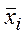 относительно
относительно  будет определять межгрупповая дисперсия s 12 ~
будет определять межгрупповая дисперсия s 12 ~ 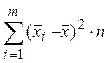 , где
, где 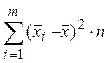 – межгрупповая вариативность. В свою очередь, внутригрупповая дисперсия s 22 ~
– межгрупповая вариативность. В свою очередь, внутригрупповая дисперсия s 22 ~  , где
, где  – внутригрупповая вариативность, в силу предположения равенства групповых дисперсий может считаться константой, и поскольку не зависит от номера группы i, то будет равняться средней групповой дисперсии. Следовательно, с ростом s 12 отношение s 12/ s 22 растет. Поэтому в качестве правостороннего критерия для проверки Н 0 используется критерий K = s 12/ s 22, имеющий распределение Фишера-Снедекора со степенями свободы k 1 = m – 1 и k 2 = mn – m = m (n – 1).
– внутригрупповая вариативность, в силу предположения равенства групповых дисперсий может считаться константой, и поскольку не зависит от номера группы i, то будет равняться средней групповой дисперсии. Следовательно, с ростом s 12 отношение s 12/ s 22 растет. Поэтому в качестве правостороннего критерия для проверки Н 0 используется критерий K = s 12/ s 22, имеющий распределение Фишера-Снедекора со степенями свободы k 1 = m – 1 и k 2 = mn – m = m (n – 1).
Напомним, что число степеней свободы определяется как общее число наблюдений (объем выборки) минус число связывающих их уравнений. Поэтому:
Ø для несмещенной оценки общей дисперсии s 2 по общей выборочной дисперсии 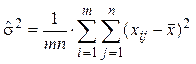 , включающей mn результатов наблюдений, связанных одном уравнением
, включающей mn результатов наблюдений, связанных одном уравнением  =
=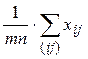 , число степеней свободы равно mn – 1, и соответственно s 2 =
, число степеней свободы равно mn – 1, и соответственно s 2 =  ;
;
Ø для несмещенной оценки групповой дисперсии si 2 по выборочной группой дисперсии  , включающей п результатов наблюдений в i -йгруппе, связанных для этой группы одним уравнением
, включающей п результатов наблюдений в i -йгруппе, связанных для этой группы одним уравнением 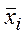 =
= 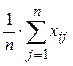 , число степеней свободы равно п – 1, и соответственно si 2 =
, число степеней свободы равно п – 1, и соответственно si 2 =  ;
;
Ø для несмещенной оценки межгрупповой дисперсии s 12 по выборочной межгрупповой дисперсии 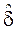 2 =
2 =  =
=  , включающей т выборочных групповых средних
, включающей т выборочных групповых средних 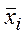 , связанных одним уравнением
, связанных одним уравнением  =
=  число степеней свободы равно k 1 = m – 1, и соответственно s 12 =
число степеней свободы равно k 1 = m – 1, и соответственно s 12 = 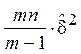 =
= 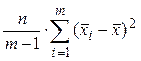 ;
;
Ø для несмещенной оценки внутригрупповой дисперсии s 22 по выборочной внутригрупповой дисперсии 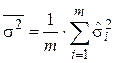 =
= 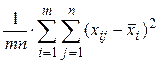 , включающей результаты объединенной выборки объемом тп, связанных между собой m уравнениями:
, включающей результаты объединенной выборки объемом тп, связанных между собой m уравнениями: 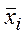 =
= 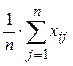 , число степеней свободы равно k 2 = mn – m, и соответственно s 22 =
, число степеней свободы равно k 2 = mn – m, и соответственно s 22 =  .
.
При этом выполняется правило сложения выборочных дисперсий:  +
+  =
=  .
.
Доказательство. Докажем справедливость тождества  +
+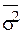 =
= , т.е., что
, т.е., что 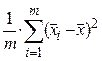 +
+ =
=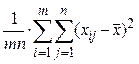 , или
, или  =
=  . Т.о., должно выполняться равенство
. Т.о., должно выполняться равенство 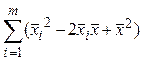 =
= 
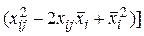 =
= 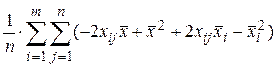 . Выполняя в левой части суммирование по индексу i, а в правой части по индексу j, получаем:
. Выполняя в левой части суммирование по индексу i, а в правой части по индексу j, получаем:  =
= 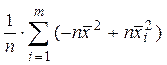 , или
, или  =
=  , или
, или 
 , что и требовалось доказать.
, что и требовалось доказать.
Т.о., K н= s 12/ s 22, а критическая точка соответствующего критерия K кр= F a(k 1 = m – 1; k 2 = mn – m). Если K н < K кр, то гипотеза Н 0 принимается, т.е. фактор А не влияет на признак генеральной совокупности; если же K н ≥ K кр, то следует учитывать воздействие на признак фактора А.
В терминах дисперсионного анализа несмещенная оценка межгрупповой дисперсии s 12 = 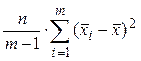 называется факторной дисперсией (именно факторная дисперсия может содержать информацию о влиянии фактора А на признак генеральной совокупности), а несмещенная оценка внутригрупповой дисперсии s 22 =
называется факторной дисперсией (именно факторная дисперсия может содержать информацию о влиянии фактора А на признак генеральной совокупности), а несмещенная оценка внутригрупповой дисперсии s 22 =  =
= 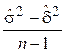 называется остаточной дисперсией (величина этой дисперсии характеризует влияние на признак всех других, отличных от А,неучтенных факторов).
называется остаточной дисперсией (величина этой дисперсии характеризует влияние на признак всех других, отличных от А,неучтенных факторов).
3o. Расчетные формулы и схема дисперсионного анализа
Для ускорения расчетов рекомендуется использовать следующую схему проведения однофакторного дисперсионного анализа при выполнении соответствующих требований для этого анализа и равенства числа наблюдений на каждом уровне воздействующего фактора:
1) Найти сумму наблюдаемых значений для каждого уровня воздействующего на признак фактора и сумму квадратов этих значений: Ti =  , Pi =
, Pi =  , где п – число наблюдений на каждом уровне фактора, имеющего т уровней действия; объем объединенной выборки равен п * = тп.
, где п – число наблюдений на каждом уровне фактора, имеющего т уровней действия; объем объединенной выборки равен п * = тп.
2) Найти 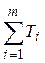 ,
,  и
и 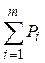 .
.
3) Найти общую вариативность признака Q = 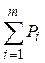 –
–  .
.
4) Найти факторную вариативность признака Q 1 =  –
–  .
.
5) Найти остаточную вариативность признака Q 2 = Q – Q 1.
6) Найти несмещенные точечные оценки факторной s 12 и остаточной s 22 дисперсий: s 12 = Q 1/(т – 1); s 22 = Q 2/(тп – т).
7) Найти наблюдаемое значение статистического критерия проверки гипотезы Н 0 о равенстве групповых средних: K н = s 12/ s 22.
8) По табличным значениям критических точек F- критерия Фишера-Снедекора для заданного уровня значимости a и степеням свободы k 1= т – 1 и k 2= тn – m найти критическое значение критерия K кр = F a(k 1 = m – 1; k 2 = mn – m).
9) Сопоставив наблюдаемое и критическое значение критерия, принять или отвергнуть гипотезу Н 0: если K н < K кр, то гипотеза Н 0 принимается, т.е. фактор А не влияет на признак генеральной совокупности; если же K н ≥ K кр, то воздействие на признак фактора значимо.
Примечание.
При использовании условных вариант uij = b ·(xij – c) следует только при расчетах Ti =  , Pi =
, Pi = 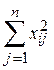 заменить xij на uij.
заменить xij на uij.
Если на различных уровнях фактора имеются наблюдения не одинакового объема, то следует внести изменения только в следующие расчетные формулы: объем объединенной выборки п * = тп заменить на п * =  , где ni – объем выборки на i -м уровне действия фактора,
, где ni – объем выборки на i -м уровне действия фактора, 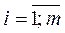 ; Ti =
; Ti =  , Pi =
, Pi =  , Q 1 =
, Q 1 =  –
– 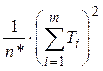 .
.
Пример 1. За 3 месяца летнего сезона в 4-х санаториях, ранжированных по возрастанию объема предоставления лечебных процедур, определена заполняемость в процентах:

| июнь | июль | август |
| А | |||
| В | |||
| С | |||
| D |
Считая, что требования к дисперсионному анализу выполняются, проверить на уровне значимости a = 0,05 гипотезу о равенстве средней заполняемости этих санаториев в летний сезон.
Решение. В данной задаче фактор А – предоставляемые оздоровительные процедуры; месяцы – временные моменты наблюдений. Уровни фактора – объемы соответствующих услуг в каждом санатории. Т.о., число уровней (градаций) фактора т = 4; объем выборки на каждом уровне п = 3; объем объединенной выборки п * = тп = 12.
На 5%-м уровне значимости следует проверить гипотезу Н 0: различия в средней заполняемости 4-х санаториев не более выражены, чем случайные различия заполняемости по месяцам для каждого санатория, альтернативная гипотеза Н 1: различия в средней заполняемости санаториев более выражены, чем случайные различия заполняемости по месяцам для каждого санатория.
Для упрощения расчетов используем условные варианты uij = (xij – 70)/10. Составляем расчетную таблицу:

| Ti = 
| Pi = 
| |||
| А 1 | – 3 | – 1 | – 2 | – 6 | |
| А 2 | – 1 | ||||
| А 3 | – 1 | ||||
| А 4 | |||||
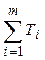 = – 3 = – 3
| 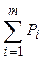 = 23 = 23
| ||||
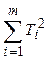 = 45 = 45
|
Находим общую вариативность признака Q =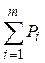 –
– = 23 – 9/12 = 22,25.
= 23 – 9/12 = 22,25.
Находим факторную вариативность признака Q 1 =  –
–  = 45/3 – 9/12 = 14,25.
= 45/3 – 9/12 = 14,25.
Находим остаточную вариативность признака Q 2 = Q – Q 1 = 22,25 – 14,25 = 8.
Находим несмещенные точечные оценки факторной s 12 и остаточной s 22 дисперсий:
s 12 = Q 1/(т – 1) = 14,25/3 = 4,75;
s 22 = Q 2/(тп – т) = 8/(12 – 4) = 1.
Находим наблюдаемое значение статистического критерия проверки гипотезы Н 0: K н = s 12/ s 22 = 4,75/1 = 4,75.
По табличным значениям критических точек F- критерия Фишера-Снедекора для уровня значимости a = 0,05 и степеням свободы k 1= т – 1 = 3 и k 2= тn – m = 8 находим K кр = F 0,05(k 1 = 3; k 2 = 8) = 4,07.
Поскольку K н > K кр, то принимается альтернативная гипотеза Н 1,т.е. воздействие на признак исследуемого фактора значимо.
Дисперсионный анализ позволяет обосновывать изменение признака с изменением градации фактора, но при этом не указывает направление этих изменений. Чтобы выявить это направление, требуется представить групповые средние и размах групповых выборочных данных или несмещенные оценки групповых СКО по градациям фактора графически. Такой график позволяет получить наглядное представление как о том, что перевешивает – тенденция, выраженная изменением характеристик признака, или вариативность признака внутри градации, так и о направлении соответствующих изменений признака.
По графику можно заключить, что значимость различий на уровнях фактора, скорее всего, объясняется тем, что при самом низком уровне медицинских услуг, популярность санатория гораздо ниже остальных случаев.
 |
Пример 2. Каждый из 6 экспертов оценил работу 20 участников выставки детского творчества. Общая вариативность оценок Q = 760, а вариативность оценок, обусловленная различием экспертов, Q 1 = 40. Какое различие превалирует: различие экспертов или различие достоинств работ, которые оценивает один и тот же эксперт?
Решение. В данной задаче переменной случайной величиной является оценка работы на выставке. Следовательно, фактор А – эксперт, оценивающий работу. Поэтому имеем т = 6 уровней фактора и п = 20 наблюдений на каждом уровне.
Влияние различия экспертов определяем по несмещенной точечной оценке факторной дисперсии s 12 = Q 1/(т – 1) = 40/5 = 8.
Влияние различия достоинств работ, проверяемых экспертом, определяем по несмещенной точечной оценке внутригрупповой (остаточной) дисперсии s 22 = Q 2/(тп – т) =(Q – Q 1)/(тп – т) = (760 – 40)/(120 – 6) = 720/144 = 5.
Т.о., различие экспертов превалирует над различием достоинств работ, которые оценивает один и тот же эксперт.
Пример 3. Для исследования влияния на изменение признака Х изменения уровня фактора А получены три выборки, соответствующие трем градациям этого фактора (см. таблицу). Выборки получены из нормально распределенных генеральных совокупностей с равными дисперсиями. Проверить гипотезу о равенстве средних на уровне значимости a = 0,025.
| ||||||||
| – | – | – | ||||||
| – |
Решение. В данной задаче т = 3 уровня действия фактора А, а объемы выборки на уровнях различны: п 1= 3; п 2= 6; п 3= 5. Объем объединенной выборки п * = п 1 + п 2 + п 3 = 3 + 6 +5 = 14.
Составляем расчетную таблицу:

| ni | Ti = 
| Pi = 
| ||||||||
| А 1 | – | – | – | ||||||||
| А 2 | |||||||||||
| А 3 | – | ||||||||||
n *= = 14 = 14
| 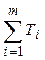 = 28 = 28
| 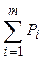 = 87 = 87
| |||||||||
 = 62,3 = 62,3
|
Находим общую вариативность признака Q =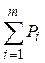 –
–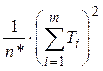 = 87 – 282/14 = 31.
= 87 – 282/14 = 31.
Находим факторную вариативность признака Q 1 =  –
– 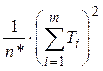 = 62,3 – 282/14 = 6,3.
= 62,3 – 282/14 = 6,3.
Находим остаточную вариативность признака Q 2 = Q – Q 1 = 31 – 6,3 = 24,7.
Находим несмещенные точечные оценки факторной s 12 и остаточной s 22 дисперсий:
s 12 = Q 1/(т – 1) = 6,3/2 = 3,15;
s 22 = Q 2/(п * – т) = 24,7/(14 – 3) ≈ 2,25.
Находим наблюдаемое значение статистического критерия проверки гипотезы Н 0: K н = s 12/ s 22 = 3,15/2,25 = 1,4.
По табличным значениям критических точек F- критерия Фишера-Снедекора для уровня значимости a = 0,025 и степеням свободы k 1= т – 1 = 2 и k 2= n * – m = 11 находим K кр = F 0,025(k 1 = 2; k 2 = 11) = 5,26.
Поскольку K н < K кр, то основная гипотеза Н 0 о равенстве групповых средних принимается,т.е. изменение уровня фактора А незначимо изменяет исследуемый признак генеральной совокупности.
 |
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 732; Нарушение авторских прав?; Мы поможем в написании вашей работы!