Лекція №16

0.4000

1.3000

2.2000

3 1 1 -1

1 -1 3 1

1 1 1 0

0.4000

1.3000

2.2000

3 1 1 7

1 -1 3 7

1 1 1 3

3 1 7 -1

1 -1 7 1

1 1 3 0

3 7 1 -1

1 7 3 1

1 3 1 0

7 1 1 -1

7 -1 3 1

3 1 1 0

3 1 1 -1

1 -1 3 1

1 1 1 0

2 2 2 2

2 8 18 32

1 2 3 4

2 4 6 8

0.8415

49 62 123

2 3 12

7 8 9

4 5 6

1 2 3

1 2 3 4

В Рабочей области (Workspace) (слева) появляется запись об имени и размере введенного вектора V. Щелкнув левой кнопкой мыши на эту запись, можно раскрыть ее и увидеть содержимое введенного вектора. Для выделения п- го элемента вектора V используется выражение V (n). Оно задает соответствующую индексированную переменную.

Задайте матрицу М размерностью 4х3

.

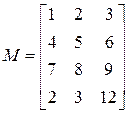Для этого в Окне команд введите:

>> M=[1 2 3; 4 5 6; 7 8 9; 2 3 12] и нажмите Enter.

В результате в Рабочей области (Workspace) появляется запись о введенной матрице M, а в Окне команд появляется результат ввода:

M =

Для выделения отдельного элемента матрицы М используется выражение вида M (j,i), где М — имя матрицы, j — номер строки иi — номер столбца.

1.3. Ознакомьтесь с правилами использования прямых вычислений. Для этого вычислим произведение введенных ранее вектора V и матрицы М (C = V x M). Очевидно, что результатом должен быть вектор-строка C размерностью 1х3 (обратите внимание, рисунок 1.1, что произведение МхV невозможно). В Окне команд наберите >> C=V*M и нажмите Enter.

Результатом будет вектор-строка

С =

Самостоятельно проведите простейшие вычисления. Например

>> 2+3

Нажмите Enter. Получим ответ

ans=

>> sin(l)

ans=

Вычислите значения синусов элементов матрицы M. Для этого введем выражение

>> MX=sin(M)

Результатом будет матрица МХ, элементами которой будут синусы элементов матрицы М.

Вычислите косинусы элементов вектора V.

>> VC=cos(V)

Ознакомьтесь с проведением операций со следующими векторами V 1 и V 2:

>> Vl=[2 4 6 8]

V1=

>> V2=[l 2 3 4]

V2 =

>> V1/V2

ans =

>> V1.*V2

ans=

>> V1./V2

ans =

Методика выполнения задания №2 «Решение системы уравнений»

Решите систему линейных уравнений

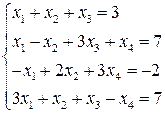
в режиме прямых вычислений методом Крамера. Для этого представим приведенную выше систему в матричной форме:

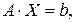
где – матрица системы; – вектор-столбец неизвестных;

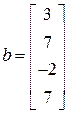– вектор-столбец свободных членов системы.

Если определитель матрицы А, , то система имеет единственное решение , или где – определитель, получаемый из определителя матрицы системы заменой i -го столбца на столбец свободных членов.

2.1. Введите матрицу системы А

>> A=[1 1 1 0; 2 -1 3 1; -1 2 0 3; 3 1 1 -1]

A =

-1 2 0 3

2.2. Вычислите определитель матрицы А, обозначив его D

>> D=det(A)

D =

-20

2.3. Введите матрицы A 1, A 2, A 3 и А 4, где соответственно 1-й, 2-й, 3-й и 4-й столбец матрицы А заменен столбцом свободных членов системы:

>> A1=[3 1 1 0; 7 -1 3 1; -2 2 0 3; 7 1 1 -1]

A1 =

-2 2 0 3

>> A2=[1 3 1 0; 1 7 3 1; -1 -2 0 3; 3 7 1 -1]

A2 =

-1 -2 0 3

>> A3=[1 1 3 0; 1 -1 7 1; -1 2 -2 3; 3 1 7 -1]

A3 =

-1 2 -2 3

>> A4=[1 1 1 3; 1 -1 3 7; -1 2 0 -2; 3 1 1 7]

A4 =

-1 2 0 -2

2.4. Вычислите определители введенных матриц:

>> D1=det(A1)

D1 =

-44

>> D2=det(A2)

D2 =

>> D3=det(A3)

D3 =

-26

>> D4=det(A4)

D4 =

-8

2.5. Вычислите корни (Х 1, Х 2, Х 3, Х 4) системы уравнений

>> X1=D1/D

X1 =

>> X2=D2/D

X2 =

-0.5000

>> X3=D3/D

X3 =

>> X4=D4/D

X4 =

2.6. Решите эту же систему уравнений матричным методом. Введите матрицу системы А и вектор-столбец свободных членов системы b.

>> A=[1 1 1 0; 1 -1 3 1; -1 2 0 3; 3 1 1 -1]

A =

-1 2 0 3

>> b=[3; 7; -2; 7]

b =

-2

2.7. MATLAB позволяет решить эту систему с помощью матричного выражения , минуя вычисление определителей. Введите это выражение:

>> X=inv(A)*b

и нажмите Enter. Ниже появится результат в виде вектора-столбца корней системы уравнений:

X =

-0.5000

Очевидно, что решение системы уравнений матричным методом и методом Крамера дает одни и те же результаты.

Методика выполнения задания №3 «Создание М-файла»

Для решения системы уравнений создадим два М-файла – файл-функцию для решения системы уравнений методом Крамера и файл-сценарий, где будут определяться исходные матрицы и вычисляться вектор корней системы.

3.1. Создайте файл-функцию. Для этого М-файла на панели инструментов нажмите Новый М-файл (New M-file), либо выполните команды File – New—M-file.

Открывается окно М-файла. Сюда введите операторы, соответствующие решению системы уравнений методом Крамера. Назовите функцию Kramer. Входными аргументами являются матрица системы А и вектор свободных членов b, выходными – вектор Х. Название функции, набор входных и выходных параметров определяются первым оператором файла-функции, имеющим следующий вид: function X = Kramer (A, b)

Далее рассчитывается определитель матрицы системы А, вводятся новые матрицы А 1, А 2, А 3 и А 4, где соответственно 1-й, 2-й, 3-й и 4-й столбцы заменяются столбцом свободных членов b, рассчитываются определители новых матриц и элементы вектора корней системы Х. Файл-функция имеет вид, представленный на рисунке 1.3.

Рисунок 1.3 – Файл-функция решения системы уравнений методом Крамера

Вектор Х представляет из себя вектор-столбец. На это указывает нумерация элементов вектора, где первая цифра номер строки, вторая – номер столбца. Если пронумеровать элементы вектора Х, как Х (1), Х (2), Х (3) и Х (4), то вектор Х будет представлять из себя вектор-строку.

3.2. Сохраните файл-функцию под именем Kramer в папке work каталога MATLAB. Важно – имя файла должно совпадать с именем функции (Kramer). Для этого нажмите в строке меню Файл (File) – Сохранить как (Save As), либо на Панели инструментов нажмите Сохранить. Появляется окно Сохранить как ((Save As) с содержимым папки work (рисунок 1.4). Нажать Сохранить (Save).

Рисунок 1.4 – Сохранение М-файла

3.3. Создайте файл-сценарий, где будут указаны исходные матрицы, произведен вызов созданного ранее файла-функции Kramer и решена система уравнений матричным методом. Блок-схема алгоритма решения задачи представлена на рисунке 1.5. Предопределенный процесс «Решение системы уравнений методом Крамера» представляет из себя файл-функцию Kramer, введенную ранее.

Аналогично пункту 3.1 создайте новый М-файл. Запишите в него соответствующий приведенному алгоритму следующий программный код:

% Решение системы уравнений

A=[1 1 1 0; 1 -1 3 1; -1 2 0 3; 3 1 1 -1]

b=[3; 7; -2; 7]

% Решение методом Крамера

Xk=Kramer(A,b)

% Решение матричным методом

Xm=inv(A)*b

3.4. Запустите на выполнение файл-сценарий. Для этого в строке меню выберите Отладка (Debug) – Сохранить и запустить (Save and Run). Следует помнить, что на решение запускается именно файл-сценарий, а не файл-функция. Происходит выполнение программы. Результаты отображаются в основном окне MATLAB.

Рисунок 1.5 Блок-схема алгоритма

решения задачи

В Окне команд отображаются результаты выполнения каждой строки программы, где в конце строки не стоит знак «точка с запятой» (;). Это удобно при отладке программ. Если вы не хотите вывода промежуточных результатов, то в конце соответствующей строки программы поставьте знак «точка с запятой». Ошибки отображаются в Окне команд красным цветом.

3.5. Проанализируйте результаты расчетов. В Рабочей области (Workspace) окна MATLAB отображаются переменные и массивы, введенные в программу и рассчитанные в ней. В данном случае там будут отображаться матрица А, вектор-столбец b, векторы-столбцы результатов решения системы, методом Крамера – X_k, матричным методом X_m. Щелкнув дважды левой кнопкой мыши по любому массиву или переменной из Рабочей области, можно раскрыть их значения в специальном окне Array Editor: (рисунок 1.6).

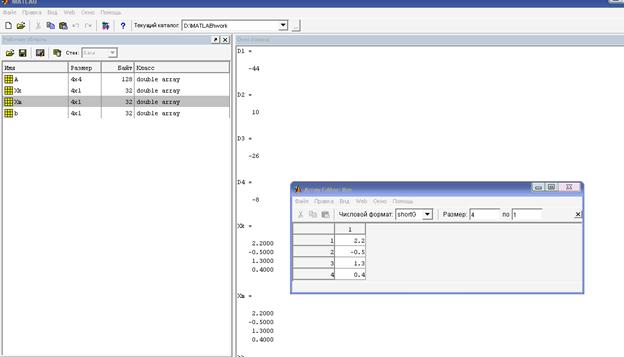
Рисунок 1.6 – Результаты решения задачи

3.6. Завершите работу MATLAB/

Задания для самостоятельной работы

1. Создайте М-файл, в котором произвольно определите следующие матрицы: C размерностью [3х4], P – [3x4], E – [5x5], F – [4x1]. Проведите следующие вычисления: 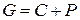; ; ; 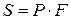определитель матрицы Е и матрицу обратную Е.

2. В соответствие с номером варианта создать М-файл для решения системы линейных уравнений методом Крамера и матричным методом.

№ варианта	Задание	№ варианта	Задание

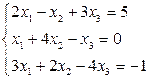
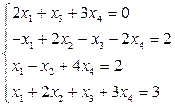
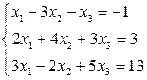
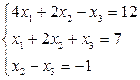
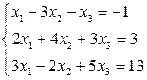
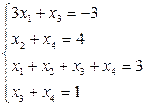
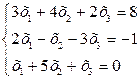
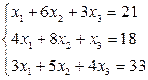
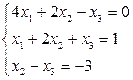
Содержание отчёта и его форма

В отчёте указывается номер лабораторной работы, её название, цель, перечень изученных в данной работе возможностей MATLAB.

Контрольные вопросы и защита работа

В ходе защиты лабораторной работы студент должен продемонстрировать электронный результат выполнения заданий. А также знать ответы на вопросы:

1. Как обозначается элемент матрицы?

2. Какие типы данных используются в MATLAB?

3. Как транспонировать матрицу, вычислить обратную матрицу?

4. Чем файл-сценарий отличается от файла-функции?

5. Как вывести промежуточные результаты выполнения программы?

6. С чего начинается ввод программы в файле-функции?

Дата добавления: 2014-01-15