Обчислення площ плоских фігур

План.

Розділ 18. Застосування визначеного інтеграла.

1. Обчислення площ плоских фігур (**).

2. Обчислення об’ємів геометричних тіл. (**).

3. Довжина дуги кривої (**).

4. Площа поверхні тіла обертання (**).

Якою б не була криволінійна фігура, обчислення площі фігури можна звести до обчислення площ розглянутих нижче фігур.

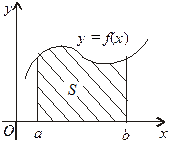
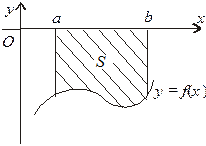
І. Фігура обмежена лініями y=f(x), y = 0, x = a, x = b (мал. 1). Функція f(x) - неперервна та 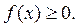Площа S такої криволінійної трапеції за геометричним змістом визначеного інтеграла така:

.

Якщо при виконанні всіх інших умов 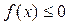(мал. 2), то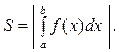

Мал. 1	Мал. 2	Мал. 3

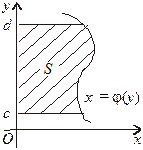
ІІ. Фігура обмежена лініями 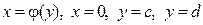(мал. 3). Функція 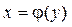— неперервна та 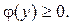Площа S такої фігури буде:

а якщо (мал. 4), то:

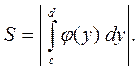
ІІІ. Фігура обмежена лініями y=f(x), Функ­ції f(x) та g(x) — неперервні та 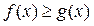для 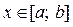(мал. 5). Площа S такої фігури визначається як різниця площ фігур аА ₂ В ₁ b та аА ₂ В ₁ b:

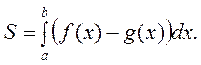
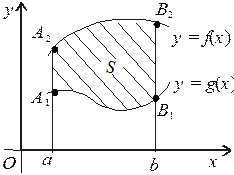
Мал. 4 Мал. 5

Приклад. Обчислити площу фігури, яка обмежена лініями 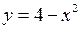та .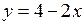

Побудуємо фігуру, як показано на малюнку. Для чого знайдемо точки перетину ліній. Для цього розв’яжемо систему:

.

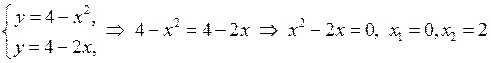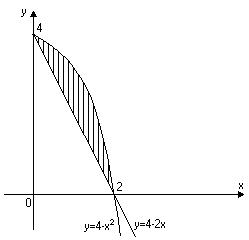Площа фігури дорівнює різниці площ двох криволінійних трапецій, площі яких можна обчислити. Одержимо:

Якщо крива задана рівняннями в параметричній формі:

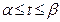
то площа криволінійної фігури обчислюється за

формулою

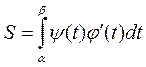
Дійсно, нехай рівняння визначають деяку у = f (x) на відрізку [ a; b ] і отже, площа криволінійної трапеції може бути обчислена за формулою

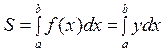
або

.

Приклад: Обчислити площу фігури, що обмежена віссю ОХ і однієї аркою циклоїди х = 5 (t – sint), y = 5 (1 – сost).

Проводимо обчислення за відповідною формулою:

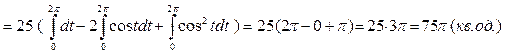
Якщо фігура обмежена лінією у полярних координатах 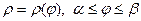, де - неперервна і невід’ємна функція на (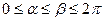). Тоді площу фігури можна обчислити за формулою:

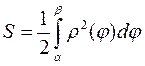
18.2 Обчислення об’ємів геометричних тіл.

Знайдемо об’єм тіла V утвореного обертанням навколо осі Ox фігури, обмеженої лініями .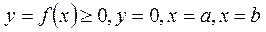

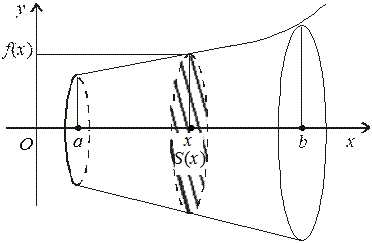
Встановлюємо, що площа поперечного перерізу S(x) в даному випадку є площа круга радіусом , тобто 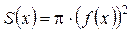, а об’єм тіла обертання за формулою буде таким:

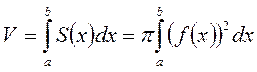
Аналогічно, об’єм тіла V утвореного обертанням навколо осі Оу фігури, обмеженої лініями x=0, 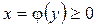, y=c, y=d матиме вигляд:

.

Рис. 11  

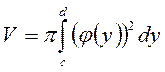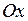Приклад. Обчислити об’єми тіл обертання навколо осей та 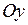фігури, яка обмежена лініями 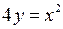та .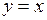

Обчислимо об’єми тіл, які утворюються при обертанні фігури навколо осей. Знайдемо точки перетину ліній:

Одержали дві точки з координатами 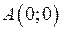та 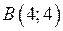. Зобразимо ці тіла схематично як показано на малюнках:

Рис. 12  

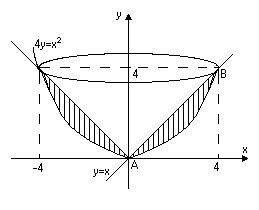
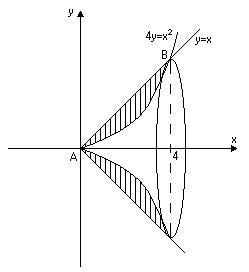
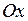1) Об’єм тіла обертання навколо осі дорівнює різниці двох об’ємів тіл:

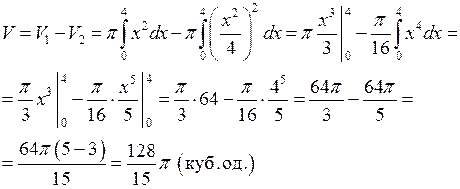
2) Аналогічно обчислюємо об’єм тіла обертання навколо осі :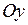

Дата добавления: 2014-01-15