Довжина дуги кривої

Нехай в прямокутних координатах на площині задана крива рівнянням у = f (x), де f (x) і f ¢(x) — неперервні на відрізку [ a; b ] функції.

Знайдемо довжину дуги АВ цієї кривої, що заключена між вертикальними прямими х = a i x = b.

Введемо позначення D у_і = f (x_i) – f (x_{i– 1}). Тоді:

.

Далі за теоремою Лагранжа знаходимо:

Отже,

Таким чином, довжина вписаної ламаної дорівнює:

.

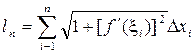За умовою, f ¢(x) — неперервна, тому функція теж неперервна. Отже, існує границя написаної інтегральної суми, який дорівнює визначеному інтегралу:

Якщо крива задана рівняннями в параметричній формі:

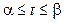, , де j(t), y(t) — неперервні функції з неперервними похідними, причому j(t) ¹ 0, t Î [ a; b ]. В цьому випадку визначають деяку функцію у = f (t) — неперервну і мають неперервну похідну

.

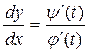Нехай а = j(a), b = j(b). Тоді зробив в інтегралі підстановку х = j(t), dx = j¢(t)dx, отримаємо:

або

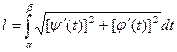
Приклад: Обчислити довжину дуги астроїди

х = 5cos³ t, y = 5sin³ t

Крива симетрична відносно обох координатних осей, тому обчислюємо спочатку довжину її четвертої частини, розташованої в першої чверті. Знаходимо

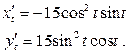
Параметр t буде змінюваться від 0 до .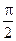

Отже:

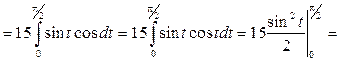
(од.)

Зауваження. Якщо задана крива параметричними рівняннями у просторі:

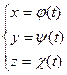то довжина дуги обчислюється за формулою:

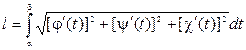
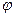Якщо фігура обмежена лінією у полярних координатах , де - полярний радіус, - полярний кут, то довжина дуги дорівнює:

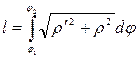
Приклад: Знайти довжину кардіоди .

Змінюючи полярний кут q від 0 до p отримаємо половину шуканої довжини.

.

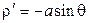Дата добавления: 2014-01-15