Учет продольных сил в расчетах сооружений методом перемещений

Необходимость учета продольных сил при расчете стержневых систем методом перемещений требует особого подхода к определению количества неизвестных в решаемых задачах. При этом формула (19.1) остается справедливой, т.е. по-прежнему

.

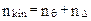Число неизвестных угловых перемещений n_θ остается таким же, как и в случае, когда влиянием продольных сил на конечный результат расчета мы пренебрегаем, т.е. оно равно количеству жестких узлов сооружения. В рассматриваемом случае иным становится число неизвестных линейных перемещений узлов системы n_Δ, которое определяется по шарнирной схеме сооружения, образуемой теперь не только введением режущих цилиндрических шарниров в жесткие узлы, но и удалением тех элементов, где требуется учесть продольные силы.

Пример 19.9.1. Определить степень кинематической неопределимости рамы, изображенной на рис. 19.27,а с учетом влияния продольных сил во всех стержнях и для ее расчета выбрать основную систему метода перемещений.

Шарнирную схему рамы образуем введением во все жесткие узлы, включая и опорные, цилиндрических шарниров и удалением стержней 1А, 12, 2В (рис. 19.27,б). Степень свободы этой шарнирной схемы определим по формуле (19.2):

W = 2Y − C − C_o = 2 ∙ 4 − 0 − 4 = 4.

Рис. 19.27

Степень кинематической неопределимости рамы равна

Основная система метода перемещений показана на рис. 19.27,в.

Пример 19.9.2. Определить степень кинематической неопределимости комбинированной системы с учетом влияния продольных сил в стержнях 1А и 13 (рис. 19.28,а) и выбрать основную систему метода перемещений для ее расчета.

Рис. 19.28

Шарнирная схема заданной стержневой системы показана на рис. 19.28,б. Обращаем внимание, что при образовании этой шарнирной схемы стержни 1А и 13 удалены. Степень свободы шарнирной схемы

W = 2Y − C − C_o = 2 ∙ 6 − 5 − 5 = 2.

Степень кинематической неопределимости рамы

Основная система метода перемещений изображена на рис. 19.28,в.

Чаще всего продольные силы при расчетах сооружений учитываются в незагруженных элементах, имеющих на концах цилиндрические шарниры. Продольную силу в таких элементах от взаимного смещения их концов в направлении оси на величину, равную Δ определим методом сил (рис. 19.29,а).

Рис. 19.29

Основная система метода сил показана на рис. 19.29,б. Реакцию в удаленной связи определим из условия

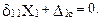(19.25)

Используя эпюру продольных сил от X₁=1 (рис. 19.29,в,г), получим при ЕА=const:

Решив уравнение (19.25), имеем:

,

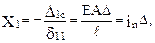где – погонная жесткость стержня при его продольных деформациях.

Окончательную эпюру продольных сил определим с помощью соотношения

N = N₁ X₁ (рис. 19.29,д).

Дата добавления: 2014-01-15