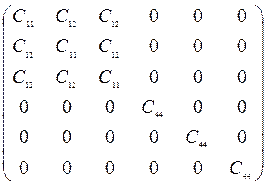Расчет упругих модулей кристалла

Расчет дисперсионных соотношений позволяет определить упругие постоянные кристалла. Для этого необходимо использовать континуальное приближение, в котором система дискретных атомов рассматривается как непрерывная среда. Это справедливо для случая больших длин волн (l>>2 a), что соответствует волновым векторам вблизи центра зоны Бриллюэна (k =0).

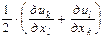Для описания упругих свойств континуума вводится величина s_i,j, называемая напряжением и характеризующая силу, действующую на площадку с нормалью, параллельной x_j, в направлении x_i. (x – координаты радиус-вектора r, описывающего положение точки в пространстве). Деформация кристалла характеризуется тензором e_k, _l =, где u_k – компоненты вектора смещения u = r’ - r, определяющего изменение положения точки в результате деформации. Согласно закону Гука деформация линейно связана с напряжением и s_i,j = C_{i , j , k , l}e_k, _l. Компоненты тензора C_{i , j , k , l} называют постоянными упругой жесткости. Для удобства записи вводятся сокращенные обозначения для пар индексов: 11º1, 22º2, 33º3, 23=32º4, 31=13º5, 12=21º6. Например C _1,1,2,1º С _1,6. С учетом симметрии в кубических кристаллах от нуля отличны только 12 компонент тензора С (только 3 являются независимыми), и он имеет вид:

С = (12)

В континуальном приближении второй закон Ньютона запишется как

_. (13)

Заменяя интеграл по поверхности интегрированием по объему V и дифференцируя, получим

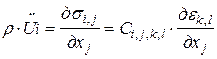_. (14)

В качестве примера рассмотрим случай распространения продольной волны вдоль кристаллографического направления [100] k =(k,0,0), u =(u, 0 0). Предполагая, что U = U ₀exp(i kx ₁-i wt), из (14) получим

w²r= С ₁₁ k ². (15)

Аналогичным образом можно найти дисперсионные соотношения и для волн с другим направлением распространения и типом поляризации.
С учетом (8) для кубических кристаллов можно получить:

а) скорость (звуковой) волны в направлении [100]

- поперечная волна ,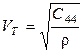

(16)

- продольная волна ;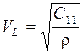

б) скорость волны в направлении [110]

- поперечная волна,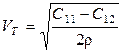

(17)

- продольная волна ;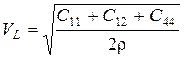

в) скорость волны в направлении [111]

- поперечная волна ,

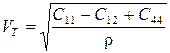(18)

- продольная волна .

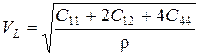Здесь C_ij - компоненты тензора упругой жесткости кристалла. Отметим, что объемный модуль упругости кубических кристаллов определяется выражением:

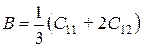. (19)

3. Программа работы.

1) Используя данные таблицы 1 (см. Приложение) провести расчет частотного спектра колебаний для кристалла вольфрама (W). Построить дисперсионные зависимости для продольных и поперечных волн в направлениях [100], [111]. Построить зависимости V (k), скорости звука сравнить с данными таблицы 2. Рассчитать значения констант упругой жесткости и сравнить с экспериментальными данными (таблица 2, Приложение). Вычислить значение объемного модуля упругости.

2) Рассчитать максимальные частоты продольных и поперечных колебаний, а также скорости переноса энергии для направлений [100], [111] для одноатомных кристаллов с ГЦК структурой (см. таблицу 1, Приложение). Полученные результаты изобразить графически. Значения скоростей сравнить с экспериментальными данными (таблица 2, Приложение).

3) Провести моделирование упругих деформаций в кристалле свинца (Pb). Для этого, изменяя значение постоянной решетки в пределах + 10% от указанной величины, рассчитать максимальные частоты продольных и поперечных колебаний, а также скорости звука для направлений [100], [111]. Полученные результаты изобразить графически.

4. Описание лабораторного оборудования

Расчеты производятся по оригинальной программе “Phonon2” на персональной ЭВМ. Оформление отчета проводится с использованием программ Word, Origin.

5. Содержание отчета

Название и цель работы

Основные соотношения, используемые для расчетов

Результаты расчета

Полученные графические зависимости

Выводы

6. Контрольные вопросы

Каков вид зависимости частот колебаний от волнового вектора в модели одноатомной цепочки, одноатомной трехмерной решетки?

Как зависит скорость переноса энергии от волнового вектора?

Как определить упругие постоянные одноатомного кристалла, зная зависимость скорости переноса энергии от волнового вектора?

В чем особенность колебаний с волновым вектром на границе зоны Бриллюэна?

ПРИЛОЖЕНИЕ

Таблица 1. Структурные характеристики и силовые постоянные одноатомных кристаллов

Кристалл (тип кристаллической решетки)	Масса атома, 10^-26 кг	Силовые постоянные взаимодействия соседних атомов)^*, Н/м	Постоянная решетки, [1]	Плотность, кг/м^3 [1]
		Продольные волны	Поперечные волны
Li (ОЦК)	1,15	0,85 [100] 1,13 [111]		3,491
Nb (ОЦК)	15,42	23,8 [100] 31,66 [111]	4,09 [100] 5,44 [111]	3,30
Mo (ОЦК)	15,93	63,5 [100] 84,5 [111]	18,01 [100] 23,96 [111]	3,15
W (ОЦК)	90,52	82,01 [100]   109,1 [111] 27.33	25,18 [100] 74.66 33,48 [111] 24.88	3,16
Ni (ГЦК)	9,74	21,09 [100] 42,19 [110]	6,89 [100] 13,77 [110]	3,52
Pd (ГЦК)	17,67			3,89
Pt (ГЦК)	32,28	33,04 [100] 66,09 [110]	5,88 [100] 11,75 [110]	3,92
Cu (ГЦК)	10,60	17,66 [100] 35,33 [110]	14,99 [100] 29,99 [110]	3,61
Ag (ГЦК)	17,90	13,87 [100] 27,74 [110]	2,71 [100] 5,41 [110]	4,09
Au (ГЦК)	32,70	20,62 [100] 41,24 [110]	2,83 [100] 5,66 [110]	4,08
Pb (ГЦК)	34,40	6,55 [100] 13,10 [110]	0,69 [100] 1,38 [110]	4,95

^*) Силовые постоянные взаимодействия соседних атомов оценены с использованием значений скоростей распространения акустических колебаний в изотропной среде.

Таблица 2. Скорость распространения акустических колебаний и упругие постоянные в одноатомных кристаллах

Кристалл (тип кристаллической решетки)	Скорости распространения акустических колебаний (в условиях изотропной среды), м/с [2]	Постоянные упругой жесткости, 10^11Н/м^2 [1]	Объемный модуль упругости, 10^11Н/м^2
	Vl	Vt	C11	C12	C44
Li (ОЦК)						0,116
K (ОЦК)			0,0370	0,0314	0,0188	0,032
V (ОЦК)			2,280	1,187	0,426	1,619
Nb (ОЦК)						1,702
Mo (ОЦК)						2,725
W (ОЦК)			5,233	2,045	1,607	3,232
Ni (ГЦК)			2,508	1,500	1,235	1,860
Pd (ГЦК)			2,271	1,761	0,717	1,808
Pt (ГЦК)						2,783
Cu (ГЦК)			1,684	1,214	0,754	1,370
Ag (ГЦК)			1,240	0,937	0,461	1,007
Au (ГЦК)			1,923	1,631	0,420	1,732
Pb (ГЦК)			0,495	0,423	0,149	0,430

Список рекомендуемой литертуры

1. Ч. Киттель. Введение в физику твердого тела. М.: Наука, 1978. 792с.

2. Павлов П.В., Хохлов А.Ф. Физика твердого тела. М.: Высшая школа, 1985. 384с.

3. Приборы для неразрушающего контроля материлов и изделий. Справочник. Кн.2. под ред. В.В. Клюева. М. Машиностроение, 1986. 352 с.

4. Брандт Н.Б., Чудинов С.М. Электроны и фононы в металлах. М.: МГУ,1990, 335с.

5. А. М. Стоунхэм. Теория дефектов в твердых телах. Т.1. М.: “Мир”, 1978 г. 570 с.

6. У. Харрисон. Теория твердого тела. М.: “Мир”, 1978 г. 580 с.

Дата добавления: 2014-01-15