Механические свойства материалов

КИНЕМАТИЧЕСКИЕ ЦЕПИ

Кинематическая пара является наиболее простым механизмом, позволяющим увеличить объем движения рычагов. В организме используются более сложные конструкции - кинематические цепи (подвижное сочленение более чем двух звеньев), которые существенно расширяют объем движения в опорно-двигательном аппарате.Типичным примером кинематической цепи служит верхняя и нижняя конечность, позвоночник и др. Так, в верхней конечности звеньями цепи являются плечо, предплечье, кисть, фаланги пальцев. Объем движения в кинематической цепи значительно возрастает, поскольку увеличивается число степеней свободы в каждом сочленении и соответствующие диапазоны изменения независимых координат. В принципе весь скелет следует рассматривать как сложную кинематическую цепь, составленную из отдельных подвижных костей. Как показывают теоретические оценки, общее число степеней свободы скелета с учетом всех возможных движений в суставах достигает 240.

Механические свойства тканей организма (упругость, эластичность, прочность, твердость и др.) обеспечивают возможность выполнения тканями и органами их физиологических функций. К примеру, высокая упругость и прочность костной ткани обеспечивает опорную функцию скелета, сохранение формы организма в поле сил тяжести. При заболеваниях эти свойства изменяются, а их определение позволяет выявлять наличие и оценивать степень выраженности патологического процесса. Во врачебной практике широко распространен способ мануальной (от слова manus - рука) диагностики - пальпация. В данном случае врач производит давление пальцами и ладонью руки на поверхность и по сопротивлению оценивает плотность, эластичность, пластичность, упругость тех тканей и органов, которые находятся под пальпируемым участком.

Для исследования механических свойств любых материалов разработана специальная теория сопротивления материалов. В связи с исключительной важностью этой проблемы в медицине к настоящему времени создано и успешно развивается биофизическое направление - биосопромат - теоретические положения, описывающие механические свойства тканей организма. Рассмотрим некоторые понятия и теоретические представления сопромата.

Все материальные тела испытывают воздействие внешних сил при контакте с другими телами или со стороны физических полей. Изменение размеров и формы материальных тел при воздействии внешних сил называется деформацией. Принято различать обратимые и необратимые деформации. Если после устранения внешнего воздействия образец самопроизвольно восстанавливает свою исходную форму, такая деформация называется обратимой. Если в этих условиях не восстанавливаются исходные геометрические размеры, деформация называется необратимой.

В зависимости от соотношения направления действующих сил и геометрических характеристик материальных объектов различают следующие виды деформаций: растяжение, сжатие, сдвиг, кручение и изгиб (см. рис. 30).

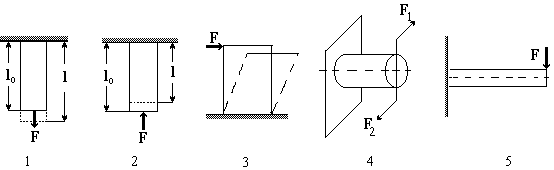
Рис. 30

Обычно механические свойства изучают на образцах правильной геометрической формы (цилиндрах, параллелепипедах). Если сила направлена вдоль оси цилиндрического образца и вызывает увеличение его длины имеет место деформация растяжения (1), если изменяется направление силы - деформация сжатия (2). Когда на тело, закрепленное на плоскости действует сила, параллельная этой плоскости, изменение формы образца называется сдвигом (3). Если к образцу приложена пара сил, лежащих в плоскости, перпендикулярной оси, наблюдается кручение (4). И наконец, когда сила перпендикулярна оси балки наблюдается изгиб (5). Количественно изменение геометрических размеров образцов оценивают с помощью абсолютной и относительной деформации. В организме человека при воздействии внешних сил и при сокращении мышц наблюдаются все перечисленные виды деформаций. Если после растяжения образца его длина стала равной l, то абсолютная деформация Dl = l - lo, где lo - исходная длина образца. Отношение абсолютной деформации к его исходному размеру e = D l/lo называется относительной деформацией. Важным понятием является внутреннее напряжение, возникающее при деформации. Как известно из физики, силы межмолекулярного взаимодействия зависят от расстояния между молекулами (см. рис. 31). Отрицательные значения сил описывают притяжение, положительные - отталкивание. Поэтому при r < r_о очень быстро увеличивается внутренняя сила отталкивания между молекулами, которые препятствуют уменьшению размеров материальных тел. При r > r_о внутренние си- Рис.

лы становятся отрицательными и способствуют притяжению между молекулами.

Рассмотрим, к примеру, растяжение цилиндрического образца под действием внешней силы Fн (см. рис. 32). Эта сила, вызывая увеличение расстояния между молекулами, способствует возрастанию внутренних сил Fв притяжения.

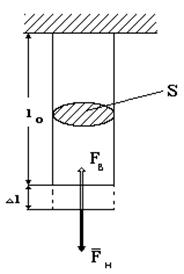
Равнодействующая всех внутренних сил Fв направлена противоположно внешней силе Fн. Когда она станет равной внешней силе, изменение размеров образца прекратится, и в материале возникает внутреннее напряжение, обусловленное деформацией. Значение напряжения определяется величиной внутренней силы, действующей на единицу прощади поперечного сечения образца S. Поскольку в равновесии (после деформации) Fн = Fв, величину напряжения можно определить как отношение внешней силы Fн к площади поперечного сечения s = Fн / S.

Введение понятий и количественный pасчет всех механических свойств материалов основано на изучении взаимосвязи между деформацией и внутренним напряжением материалов.

Рис.

Дата добавления: 2014-01-15