Группировка угловых перемещений узлов

Рассмотрим расчет рамы с вертикальной осью симметрии на произвольную нагрузку (рис. 21.1,а). Соотношение между погонными жесткостями симметрично расположенных ригелей 1А, 2В 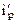и стоек 1С, 2D i_c, а также центрального ригеля 12 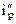, задано. Степень кинематической неопределимости рамы равна двум. На рис. 21.1,б показана основная система метода перемещений для этой рамы.

Неизвестные углы поворотов узлов 1 и 2 рассма­триваемой рамы от заданной нагрузки Z₁ и Z₂ определяются из системы канонических уравнений (см. п. 19.3 девятнадцатой лекции)

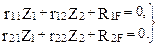(21.1)

Нетрудно убедиться в том, что в нашем случае, принимая за неизвестные углы поворота отдельных узлов, мы будем иметь полную систему уравнений (21.1), т.е. ни один из коэффициентов при неизвестных Z₁ и Z₂ не будет равен нулю (предлагаем читателям самостоятельно проверить это).

Используем симметрию рамы и произведем группировку угловых перемещений симметрично расположенных узлов 1 и 2. Каждое из уравнений системы (21.1) отрицает в основной системе метода перемещений реакции R₁ и R₂ в наложенных угловых связях 1 и 2 от их поворота на углы, равные Z₁ и Z₂, и от заданной нагрузки, т.е. первое уравнение удовлетворяет условию R₁ = 0, а второе – R₂ = 0. Эти условия будут выполнены, если в основной системе метода перемещений будем одновременно отрицать разность и сумму реакций в наложенных связях 1 и 2, т.е. если будем отрицать групповые реакции

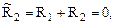
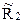Групповым реакциям и соответствуют групповые угловые перемещения узлов 1 и 2 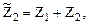которые в дальнейшем будем называть групповыми неизвестными метода перемещений.

В единичном состоянии основной системы метода перемещений неизвестному групповому перемещению соответствует одновременный поворот угловой связи, наложенной на узел 1, по часовой стрелке на угол, величина которого равна единице, и угловой связи, наложенной на узел 2, – против часовой стрелки на такой же угол – другими словами, симметричная деформационная схема элементов рамы и симметричная групповая эпюра изгибающих моментов (рис. 21.1,в,г). Аналогично, групповому неизвестному перемещению в основной системе метода перемещений соответствует обратно симметричная схема деформаций и обратно симметричная групповая эпюра изгибающих моментов 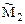(рис. 21.1,д,е).

При построении групповых эпюр изгибающих моментов и 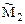для всех элементов рамы, кроме центрального ригеля 12, использованы стандартные задачи метода перемещений, рассмотренные в п. 19.4 девятнадцатой лекции. На ригеле 12 эпюры изгибающих моментов можно получить суммированием соответствующих эпюр от симметричного поворота двух угловых связей на угол θ (рис. 21.2,а) и от обратно симметричного поворота этих же связей на такой же угол (рис. 21.2,б).

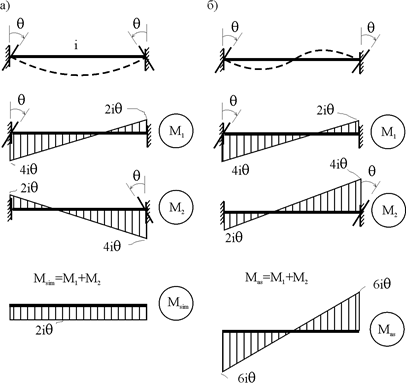
Рис. 21.2

Система канонических уравнений (21.2) для групповых неизвестных метода перемещений перепишется:

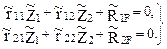(21.2)

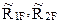Коэффициенты при неизвестных и свободные членысистемы уравнений (21.2) можно вычислить сопряжением соответствующих эпюр изгибающих моментов (см. формулы (19.11), (19.12) и (19.18) девятнадцатой лекции), либо из условия равновесия одновременно двух узлов, содержащих симметрично расположенные связи.

Так как групповые эпюры и носят соответственно симметричный и обратно симметричный характер, то

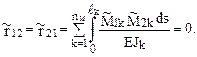
С учетом последнего обстоятельства система уравнений (21.2) распадается на два независимых друг от друга уравнения:

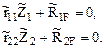
При построении эпюр внутренних усилий в заданном сооружении групповые неизвестные метода перемещений используются как обычные. В частности, для рамы, показанной на рис. 21.1,а имеем:

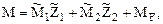
где M_F – эпюра изгибающих моментов в основной системе метода перемещений от заданной нагрузки.

Дата добавления: 2014-01-15