Группировка линейных перемещений узлов

Группировка линейных перемещений симметрично расположенных узлов целесообразна, если при выборе основной системы метода перемещений наложение линейных связей на узлы производится без нарушения симметрии сооружения.

Рис. 21.3

Поясним это на примере рамы, имеющей вертикальную ось симметрии (рис. 21.3,а). Степень кинематической неопределимости этой рамы равна четырем (n_θ = 2, n_Δ = 2). Для ее расчета предлагается симметричная основная система метода перемещений, показанная на рис. 21.3,б. Рассмотрим группировку линейных перемещений узлов А и В рамы, приняв за неизвестные групповые линейные перемещения, а именно: сумму и разность линейных перемещений этих узлов Z₁ и Z₂, т.е.

,

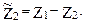
В единичном состоянии основной системы метода перемещений неизвестному групповому перемещениюсоответствует одновременное смещение линейных связей 1 и 2, наложенных на узлы А и В, направо на величину, равную единице, другими словами, обратно симметричная деформационная схема элементов рамы и обратно симметричная групповая эпюра изгибающих моментов (рис. 21.4).

Неизвестному групповому перемещению в основной системе метода перемещений соответствует одновременное единичное смещение связей 1 и 2 в разные стороны, т.е. симметричная деформационная схема и симметричная групповая эпюра изгибающих моментов 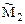(рис. 21.5).

Рис. 21.4

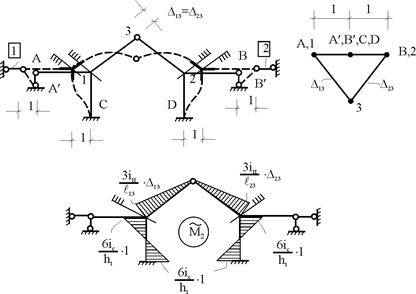
Рис. 21.5

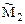Учитывая обратно симметричный характер групповой эпюры изгибающих моментов и симметричный –, получим

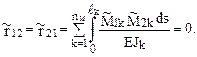
Следствием группировки линейных и угловых перемещений симметрично расположенных узлов сооружения является упрощение системы канонических уравнений метода перемещений за счет исключения из нее нулевых побочных коэффициентов.

Дата добавления: 2014-01-15