Логарифмический профиль скорости

Закономерности пути смешения и коэффициента турбулентного переноса при движении жидкости около неподвижной стенки принципиально отличаются от закономерностей турбулентного движения при свободном движении жидкости вдалеке от твердых поверхностей. Наличие молекулярной вязкости на процессы турбулентного переноса значительно усложняет изучение «пристенной» турбулентности.

Рассмотрим плоское осредненное движение жидкости, заполняющей все полупространство, около неподвижной твердой стенки. Примем, что ось 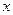направлена вдоль стенки, а ось 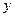- по нормали к ней. Объемными силами пренебрегаем. В этом случае любые два, поперечные линиям тока сечения, идентичны в кинематическом и динамическом смысле. То есть все производные по 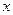равны нулю, а элементы движения могут зависеть только от координаты .

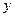Для сравнения рассмотрим ламинарное и осредненное турбулентное движения такого типа.

Ламинарное движение.

Замечая, что

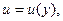
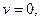
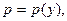
приведем уравнения ламинарного движения к виду

.

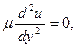
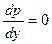Отсюда следует

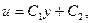
В рассматриваемом случае безграничного движения, единственным граничным условием является

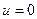при ,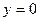

что дает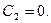Для определения 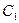примем в качестве заданной постоянной напряжение трения на стенке

.

Тогда распределение скоростей в ламинарном потоке будет

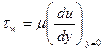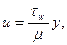
и профиль скорости окажется линейным, а напряжения трения между любыми двумя слоями жидкости одинаково и равно напряжению трения на стенке.

Рассмотрим теперь турбулентное движение жидкости около стенки, которое в нашем случае описывается уравнениями Рейнольдса.

,

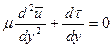где 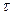- чисто турбулентное трение.

Интегрируя это уравнение один раз, получим:

.

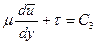Замечая, что напряжение турбулентного трения 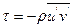на стенке равно нулю, так как на стенке не могут существовать нормальные к ней пульсации 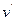, получим 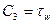и, следовательно,

.

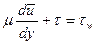В непосредственной близости к стенке турбулентное трение 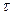значительно меньше слагаемого 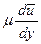, соответствующего молекулярному трению. Пренебрегая в пристеночной области турбулентным трением по сравнению с молекулярным, получим:

.

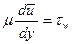Проинтегрировав данное уравнение и определив произвольную постоянную из условия равенства нулю осредненной скорости на стенке, будем иметь:

.

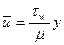Отсюда видно, что решение (3) в пристеночной области совпадает по виду с (1).

В области, удаленной от стенки, слагаемое 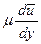мало по сравнению с турбулентным трением 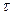и может быть опущено. Если задать турбулентное трение формулой Прандтля, получим:

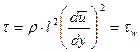
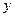Расстояние данной точки от твердой стенки является единственной характерной для потока длиной. Поэтому Прандтль положил, что в этом простейшем случае путь смешения пропорционален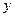

.

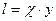Коэффициент 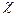представляет собой числовую константу, определяемую из опыта.

Уравнение (4) при наличии соотношения (5) легко интегрируется, его интеграл записывается в виде:

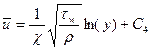
Сравнение профиля осредненных скоростей (6) с распределением скоростей при ламинарном потоке, показывает принципиальное отличие турбулентного потока от ламинарного.

Существенно, что логарифмический профиль скорости вблизи стенки (6) сохраняется не только в данной простейшей задаче, но и в более сложных случаях. Для определения произвольной постоянной 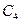нельзя воспользоваться условием на стенке, так как в пристеночной области формула (6) несправедлива. Единственной возможностью определения данной постоянной является сращивание логарифмического решения (6) с линейным (3).

Примем следующую упрощенную схему. Представим поток разбитым на две резко различные по структуре области: тонкую пристеночную область чисто вязкого движения – вязкий (ламинарный) подслой – и область не зависящего от вязкости полностью турбулентного движения – турбулентное ядро потока. В порядке уточнения такой схемы можно было бы ввести еще промежуточную между вязким подслоем и турбулентным ядром потока переходную область, где наряду с турбулентным трением учитывалось бы и молекулярное трение. Введение такой переходной области оказывается полезным при изучении тепломассопередачи. При изучении же гидродинамики потока, как показывают опыты, можно использовать схемой двух областей: вязкого подслоя и турбулентного ядра.

Обозначим через 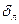толщину вязкого подслоя, а через 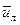скорость на границе между вязким подслоем и турбулентным ядром потока, общую для обеих областей. Движение в вязком подслое характеризуется величиной напряжения трения на стенке 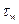и физическими константами жидкост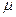и и 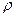. Рассматривая эти три величины с точки зрения теории размерности, составим из них две возможные комбинации:

,

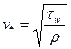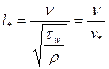
Первая из этих величин имеет размерность скорости, хотя по своей природе состоит из динамических величин: напряжения трения и плотности; поэтому ее называют «динамическая скорость». Вторая имеет размерность длины и по той же причине называется «динамическая длина». С помощью теории подобия легко показывается, что в рамках вязкого подслоя любая величина, имеющая размерность скорости будет отличаться только числовым множителем от , а любая величина, имеющая размерность длины, будет отличаться только числовым множителем от .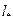

Отсюда следует, что толщина вязкого подслоя 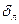и скорость на границе подслоя 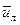должны быть пропорциональны динамической длине 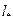и динамической скорости . Докажем, что коэффициенты пропорциональности у них одинаковы.

Положим

,

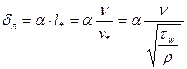где 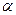- безразмерная константа. Тогда по (3) получим:

.

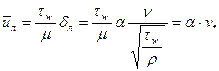Пользуясь полученными соотношениями, определяем константу 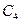в формуле (6) из условий на границе вязкого подслоя.

.

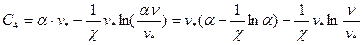Подставляя в формулу (6) найдем:

,

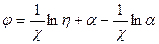где , .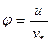

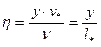Переходя от натуральных логарифмов к десятичным, получим:

.

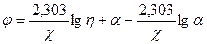И. Никурадзе проводил опыты над турбулентным движением воды в длинных цилиндрических трубах круглого сечения в широком диапазоне чисел Рейнольдса от критического их значения, до чисел Рейнольдса равных 3,24*10⁶. На графике приводятся результаты его точных и систематически поставленных опытов по измерению скоростей в сечении трубы. Как это следует из графика, экспериментальные точки вполне располагаются по прямой, соответствующей логарифмическому профилю скоростей.

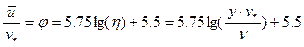
Принципиальное значение имеет тот факт, что логарифмическая формула сохраняет свою форму для всех рейнольдсовых чисел течения, или, как принято говорить, универсальна.

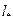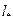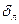Структура логарифмической формулы такова, что влияние числа Рейнольдса, то есть вязкости, полностью входит в масштабы длин и скоростей ; это и делает формулу (9) универсальной. С физической стороны указанное свойство логарифмической формулы объясняется наличием ламинарного подслоя, в котором сосредоточено все влияние вязкости, и отмеченной ранее пропорциональностью масштабов и толщине подслоя и скорости на его внешней границе .

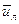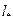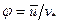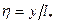Масштабы и называются универсальными, а величины и соответственно универсальными скоростью и координатой.

Сравнивая формулу (9) с теоретически выведенной формулой (8) убеждаемся в том, что для количественного совпадения необходимо положить:

.

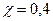
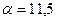Экспериментальные данные отклоняются от (9) лишь в области сравнительно малых значений 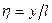, соответствующих точкам близким к стенкам трубы, где уже становится заметным влияние вязкости. Можно еще заметить намечающееся отклонение экспериментальных точек вверх от прямой (9) в правой части графика (при 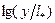> 4,4). Это отклонение объясняется отклонением рассмотренного плоского движения от движения в трубе

(влиянием противоположной стенки трубы).

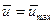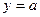Хотя логарифмическая формула и дает погрешность в области близкой к оси трубы, тем не менее, применим формулу (8) к оси трубы, полагая при , где 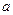- радиус трубы.

Вычитая почленно из данной формулы формулу (8), получим формулу дефекта скорости:

.

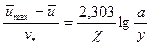Подставляя сюда 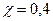, окончательно найдем:

.

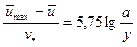Константы 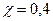и 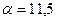представляют две основные эмпирические постоянные, характеризующие турбулентное движение.

Таким образом, проведенный упрощенный теоретический анализ позволяет уловить основные закономерности распределения скорости при турбулентном движении в круглой трубе. Необходимость использования двух эмпирических констант сохраняется и в более точных полуэмпирических теориях турбулентности.

В своей центральной части, формула (10) близка к классическому профилю, введенному в гидравлику Дарси.

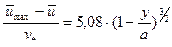
Соотношение для определения средней скорости потока по сечению имеет вид:

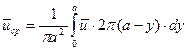
Взяв интеграл и принимая 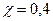, получим:

.

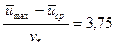Это формула связи между максимальной (на оси трубы) и средней по сечению трубы скоростью хорошо подтверждается на опыте. В отличие от ламинарного движения в круглой трубе, при котором 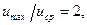в турбулентном движении это отношение уменьшается с ростом числа 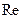от 1,3 при малых его значениях (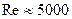), до 1,15 при сравнительно больших (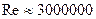). Это говорит о резком отличии формы профиля скорости в турбулентном движении, от параболы скоростей в ламинарном движении. В турбулентном движении профили скорости являются более заполненными, чем при ламинарном движении, причем степень заполнения возрастает с ростом числа .

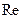Дата добавления: 2014-01-15