Гладких и шероховатых труб

Логарифмические и степенные формулы сопротивления

Выведенные формулы распределения скоростей содержат неизвестную заранее величину , связанную с напряжением трения на стенке трубы. Чтобы сделать задачу определенной, необходимо найти дополнительную связь между величинами и (или ). Такая связь задается формулой сопротивления трубы турбулентному движению жидкости.

Задача сводится к определению зависимости коэффициента сопротивления , входящего в формулу

от числа .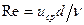

При равномерном установившемся движении жидкости в трубе движущий перепад давления уравновешивается сопротивлением трения:

.

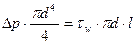Отсюда следует:

.

Подставляя это выражение в формулу (11) найдем:

.

Вспоминая еще определение , получим:

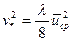и

Для вывода искомой формулы сопротивления применим (9) для оси трубы.

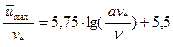
С учетом того, что 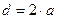и формулы (12) найдем:

,

или используя (12):

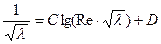
Многочисленные опыты хорошо подтверждают следующую формулу с округленными коэффициентами:

.

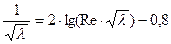Формула (13) дает связь между числом Рейнольдса и коэффициентом сопротивления в неявном виде, что неудобно для использования. Никурадзе предложил пользоваться следующей явной зависимостью:

.

В гидрогазодинамике широко используется также формула Блаузиуса:

,

которую можно применять при значениях числа 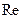< 10⁵.

Наряду с выведенными полуэмпирическими соотношениями – логарифмическим профилем скорости и логарифмической формулой сопротивления – большую роль играют чисто эмпирические степенные профили скорости и сопротивления. К числу последних относится и формула Блазиуса, которая представляет частный случай общей степенной формулы сопротивления

.

Как показывают опытные данные, с возрастанием числа Рейнольдса показатель степени m и коэффициент с изменяются. Причем m – убывает. Пользуясь экспериментальной формулой Блазиуса, Карман, из соображений размерности показал, что степенному закону сопротивления соответствует степенной профиль скоростей

,

получившей наименование закона одной седьмой.

Точно так же общей формуле (14) соответствует степенной закон скоростей

Отношение средней скорости к максимальной будет в этом случае иметь вид:

.

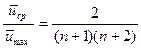Можно легко получить связь между m, n и с.

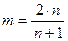
Изложенное выше относится лишь к движению в гладкой трубе. На практике приходится иметь дело с более или менее шероховатыми трубами, а также с трубами с неточной цилиндричностью, волнистостью и т.д.

Далее рассматриваются вопросы, связанные с течением жидкости в шероховатых трубах, рассматриваются опыты Никурадзе и его график.

Лекция 2

Изложенное выше относится к движению в гладкой трубе со строго цилиндрической поверхностью.

На практике приходится иметь дело с более или менее шероховатыми трубами, а также с трубами с неточной цилиндричностью внутренней поверхности – волнистостью.

Изучением влияния различного типа шероховатостей на сопротивление труб занимается гидравлика.

Предположим, что внутренняя поверхность трубы покрыта бугорками, имеющими вид зерен примерно одинакового размера. Обозначим через 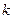высоту бугорка шероховатости (практически среднюю высоту) и условимся называть величину 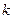, выраженную в миллиметрах, абсолютной шероховатостью, а отношение величины 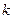к радиусу трубы 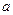- относительной щероховатостью.

В дальнейшем предполагается, что значение относительной шероховатости невелико - порядка 0.2 – 7 %. На основании экспериментальных данных, можно сделать выводы:

- относительная шероховатость не влияет на критическое число Рейнольдса перехода ламинарного режима в турбулентный; для различных кривые сходят с известной ламинарной прямой при одном и том же значении числа ;

- переходный режим также не зависит от числа относительной шероховатости;

- чем меньше относительная шероховатость, тем в большем диапазоне чисел Рейнольдса наблюдается обычное турбулентное движение, соответствующее гладким трубам; так при относительной шероховатости 0.2 %, кривая сопротивления почти до совпадает с кривой Блазиуса. Наоборот, при 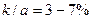кривые сопротивления пересекаются с кривыми гладких труб и резко от них отличаются;

При тем больших числах Рейнольдса, чем меньше относительная шероховатость, коэффициент сопротивления перестает зависеть от числа Рейнольдса и определяется только относительной шерозоватостью; при этом значения коэффициента сопротивления растут вместе с относительной шероховатостью.

Этим данным можно дать теоретическое обоснование, если сопоставить высоту бугорка шероховатостью 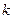с толщиной ламинарного подслоя .

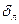Первый предельный режим:

Бугорки шероховатости погружены в ламинарный подслой. Наличие этих бугорков не нарушает ламинарного подслоя, бугорки обтекаются без отрывов и вихреобразования. В этом случае нет никакой разницы между гладкой и шероховатой трубами. Шероховатая труба является гидродинамически гладкой.

Второй предельный режим:

Бугорки шероховатости выходят за пределы ламинарного подслоя (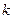»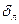). Отрывное обтекание бугорков сводит тормозящее влияние поверхности трубы к сопротивлению плохо обтекаемых тел, которое не зависит от рейнольдсова числа и пропорционально скоростному напору набегающей жидкости. Режим развитой шероховатости.

Третий промежуточный режим:

Этот режим – когда высота бугорков шероховатости имеет тот же порядок, что и толщина ламинарного подслоя. Этот режим является наиболее общим. Остальные два режима по отношению к нему служат предельнымие.

В общем случае сопротивление 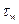по своей природе представляет отнесенное к единице площади суммарное сопротивление бугорков шероховатости. Можно допустить справедливость формулы:

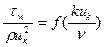
где 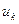- скорость на высоте бугорка, а комплекс

играет роль рейнольдсова числа обтекания бугорка.

Имеем:

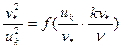
Разрешая это соотношение относительно , получим:

Вид функции Ф неизвестен и определяется из опытов. Нужно лишь отметить независимость виды функции Ф от числа Рейнольдса и шероховатости.

Воспользуемся линией вершин бугорков шероховатости 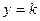, где 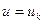, как недостающим граничным условием для определения постоянной интегрирования в выражении логарифмического профиля скоростей. Получим формулу распределения скоростей в шероховатой трубе.

Выведем формулу сопротивления

Дата добавления: 2014-01-15