Система m линейных уравнений с n переменными

Задача о раскрое материалов.

Задача об использовании ресурсов (задача планирования производства).

Примеры построения ЭММ экономических задач линейного программирования

Понятие экономико-математической модели

Существует много различных определений понятия «модель», отличающихся друг от друга. Но это понятие знакомо каждому: игрушечный корабль – модель корабля, фотоснимок пейзажа, географическая карта – модель местности, формула – математическая модель. Под моделью будем понимать условный образ какого-либо объекта, приближенно воссоздающий этот объект с помощью некоторого языка. В экономико-математ моделях объектом является экономический процесс (например, использование ресурсов, распределение изделий между различными типами оборудования и т.п.), а языком – классические и специально разработанные математические методы.

Экономико-математическая модель – математическое описание исследуемого экономического процесса или объекта. Эта модель выражает закономерности экономического процесса с помощью математических соотношений.

Процедура экономико-математ моделирования заменяет дорогостоящие и трудоемкие натуральные эксперименты расчетами. При помощи ЭВМ можно достаточно быстро и дешево произвести сравнение многочисленных вариантов планов и управленческих решений. В результате отбираются наиболее оптимальные варианты.

Для изготовления двух видов продукции П1 и П2 используют три вида ресурсов Р1, Р2 и Р3. Известны запасы этих ресурсов В1, В2 и В3 и число единиц ресурсов, затрачиваемых на изготовление единицы каждого вида продукции а11, а12, а21, а22, а31, а32. Известна также прибыль, получаемая от единицы продукции П1 и П2 – соответственно С1 и С2.

Необходимо составить такой план производства продукции, при котором прибыль от ее реализации будет макс.

ЭММ задачи:

Х1 и Х2 – число единиц продукции П1 и П2 соответственно.

F = С1*Х1 + С2*Х2 (1.1)

При ограничениях:

а11*Х1 + а12*Х2 <= В1

а21*Х1 + а22*Х2 <= В2 (1.2)

а31*Х1 + а32*Х2 <= В3

По смыслу задачи Х1>=0, X2>=0. (1.3)

Итак ЭММ задачи: найти такой план выпуска продукции Х = (Х1, Х2), удовлетворяющий системе (1.2) и условию (1.3), при котором функция (1.1) принимает макс значение.

В общей постановке ЭММ задачи об использовании ресурсов примет вид:

Найти такой план Х = (Х1, Х2, …, Хn) выпуска продукции, удовлетворяющий системе

а11*Х1 + а12*Х2 + … + а1n*Xn <= В1

а21*Х1 + а22*Х2 + … + а2n*Xn <= В2 (1.4)

………………………….

аm1*Х1 + аm2*Х2 + … + аmn*Xn <= Вm

и условию Х1>=0, X2>=0, …, Xn>=0, (1.5)

при котором функция

F = С1*Х1 + С2*Х2 + … + Сn*Xn (1.6)

принимает макс значение.

На раскрой (распил, обработку) поступает материал одного образца в количестве А единиц. Требуется изготовить из него L разных комплектующих изделий в количествах, пропорциональных числам b1, b2, … b_l (условие комплектности). Каждая единица материала м.б. раскроена N различными способами, причем использование i-го способа (i=1,2,…,n) дает а_ik единиц k-го изделия (к=1,2, …,l).

Необходимо найти план раскроя, обеспечивающий макс число комплектов.

Составим ЭММ задачи:

Обозначим Хi – число единиц материала раскраиваемых i-ым способом, и Х – число изготавливаемых комплектов изделий. Т.к. общее количество материала равно сумме его единиц, раскраиваемых различными способами, то

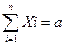(2.1)

Требование комплектности выразится уравнениями

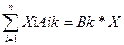(k=1,2,…, l) (2.2)

Очевидно, что Хi >=) (i=1,2,…,n) (2.3)

ЭММ задачи: найти такое решение Х=(х1, х2, …, хn), удовлетворяющее системе уравнений (2.1) – (2.2) и условию (2.3), при котором функция F = х принимает макс значение.

Эту задачу можно обобщить на случай m раскраиваемых материалов.

Пусть каждая единица j-го материала (j = 1, 2,…, m) может быть раскроена N различными способами, причем использование i-го способа (i =1,2,…,n) дает а_ijk единиц k-го изделия (к=1,2, …,l), а запас j-го материала равен Aj единиц.

Обозначим Хij – число единиц j-го материала раскраиваемого i-ым способом.

ЭММ задачи о раскрое материалов в общей постановке примет вид: найти такое решение Х=(х11, х12, …, хnm), удовлетворяющее системе

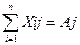(j = 1, 2,…, m),

(k=1,2,…, l)

и условию Xij >= 0, при котором функция F = х принимает макс значение.

Рассмотренные примеры задач линейного программирования позволяют сформулировать общую задачу линейного программирования.

Дана система m линейных уравнений и неравенств с n переменными

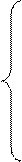а11*Х1 + а12*Х2 + … + а1n*Xn <= В1

а21*Х1 + а22*Х2 + … + а2n*Xn <= В2

………………………….

ак1*Х1 + ак2*Х2 + … + акn*Xn <= Вк

ак+1,1*Х1 + ак+1,2*Х2 + … + а к+1,n*Xn = В к+1 (1)

а к+2,1*Х1 + а к+2,2*Х2 + … + а к+2,n*Xn = В к+2

………………………….

аm1*Х1 + аm2*Х2 + … + аmn*Xn = Вm

и линейная функция

F = С1*Х1 + С2*Х2 + … + Сn*Xn (2)

Найти такое решение системы Х = (Х1, Х2, …,Xj,…, Хn), где

Хj>=0 (j = 1, 2,…, l; l<=n) (3)

при котором линейная функция F (2) принимает оптимальное (макс или мин) значение.

Система (1) называется системой ограничений, а функция F – линейной функцией, линейной формой, целевой функцией или функцией цели.

Более кратко общую задачу линейного программирования можно представить в виде:

F = 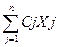à max (min)

При ограничениях:

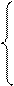
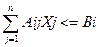(I = 1, 2, …, k)

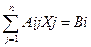(I = k+1, k+2, …, m)

Хj>=0 (j = 1, 2,…, l; l<=n)

Оптимальным решением (или оптимальным планом) задачи ЛП называется решение Х = (Х1, Х2, …,Xj,…, Хn) системы ограничений (1), при котором линейная функция (2) принимает оптимальное (макс или мин) значение.

Термины «решение» и «план» - синонимы, однако первый используется чаще, когда речь идет о формальной стороне задачи (ее математическом решении), а второй – о содержательной стороне (экономической интерпретации).

При условии, что все переменные неотрицательны (Хj>=0, j = 1, 2,…, n), система ограничений (1) состоит лишь из одних неравенств, - такая задача ЛП называется стандартной; если система ограничений (1) состоит из одних уравнений, то задача называется канонической. В приведенных выше примерах задача 1 – стандартная, 2 – каноническая. Бывает – общая.

Любая задача ЛП м.б. сведена к канонической, стандартной или общей.

Вспомогательная теорема (без доказательства):

Всякому решению неравенства

аi1*Х1 + аi2*Х2 + … + аin*Xn <= Вi (4)

соответствует определенное решение уравнения

аi1*Х1 + аi2*Х2 + … + аin*Xn + Хn+i= Вi (5)

в котором Хn+i>=0 I = 1,m (6)

и, наоборот, каждому решению уравнения (5) и неравенства (6) соответствует определенное решение неравенства (4).

Используя эту теорему, можно представить стандартную задачу (1.4) – (1.6) в каноническом виде. С этой целью в каждое из m неравенств в системе ограничений (1.4) вводятся дополнительные неотрицательные переменные Xn+1, Xn+2, Хn+m и система ограничений примет вид:

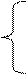а11*Х1 + а12*Х2 + … + а1n*Xn + Xn+1 = В1

а21*Х1 + а22*Х2 + … + а2n*Xn + Xn +2 = В2 …………………………………………………………….

аm1*Х1 + аm2*Х2 + … + аmn*Xn + Xn +m = Вm

Замечание. В рассматриваемой задаче все неравенства вида <=, поэтому дополнительные неотрицательные переменные вводились со знаком «+». В случае неравенства вида >= соответствующие дополнительные неотрицательные переменные вводились бы со знаком «-».

Система m линейных уравнений с n переменными имеет вид:

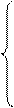а11*Х1 + а12*Х2 + …+ а1j*Xj + …+ а1n*Xn = В1

а21*Х1 + а22*Х2 + …+ а2j*Xj + … + а2n*Xn = В2

………………………….

аi1*Х1 + аi2*Х2 +…+ аij*Xj + … + а in*Xn = В i (6)

………………………….

аm1*Х1 + аm2*Х2 + … + аmn*Xn = Вm

или в краткой записи

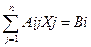(I = 1, 2, …, m)

в задачах ЛП представляют интерес системы, в которых максимальное число независимых уравнений системы меньше числа переменных. Будем полагать, что в системе (6) все m уравнений системы независимы, т.е. m < n.

Любые m переменных системы m линейных уравнений с n переменными (m < n) называются основными (базисными), если определитель матрицы коэффициентов при них отличен от нуля. Тогда остальные n - m переменных называются неосновными (или свободными).

Основными могут быть разные группы из n переменных, но общее число групп не превосходит число сочетаний .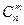

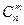= n! / ((n-m)! m!)

Пример:

Найти все возможные группы основных переменных в системе

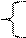х1 – х2 – 2х3 + х4 = 0 (7)

2х1 + х2 + 2х3 – х4 = 2

Решение. Общее число групп основных переменных не более чем 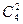= 4*3/2 = 6, т.е. возможны группы основных переменных: х1, х2; х1, х3; х1, х4; х2, х3; х2, х4; х3, х4.

Переменные х1, х2 могут быть основными, т.к. определитель матрицы из коэффициентов при этих переменных 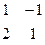= 1 * 1 – 2 * (-1) = 3 ¹ 0. рассуждая аналогично, можно найти, что могут быть основными переменные х1, х3; х1, х4, но не могут быть основными х2, х3; х2, х4; х3, х4, т.к. соответствующие определители равны 0.

х3, х4 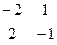= (-2) * (-1) – 2 * 1 = 0.

Существует теорема. Если для системы из m линейных уравнений с n переменными ((m < n) существует хотя бы одна группа основных переменных, то эта система является неопределенной, причем каждому произвольному набору значений неосновных переменных соответствует одно решение системы.

Пусть, например, х1, х2, …, хm – основные переменные (если это не так, то нумерацию можно изменить), то определитель матрицы

¹ 0.

Оставим в левых частях уравнений системы (6) члены с переменными х1, х2, …, хm, а члены с переменными x_m+1, x_m+2, …, x_n перенесем в правые части. Получим:

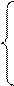
а11*Х1 + а12*Х2 + …+ а1m*Xm = В1 - а1m+1*Xm+1 - … - а1n*Xn

а21*Х1 + а22*Х2 + …+ а2m*Xm = В2 – а2m+1*Xm+1 - … - а2n*Xn

…………………………………………………………………….

аm1*Х1 + аm2*Х2 + …+ аmm*Xm = Вm - аmm+1*Xm+1 - … - аmn*Xn

Задавая неосновным переменным x_m+1, x_m+2, …, x_n произвольные значения, каждый раз будем получать новую систему с новыми свободными членами. Каждая из полученных систем будет иметь один и тот же определитель, т.е. каждая из систем будет иметь единственное решение. Так как получаемых таким образом систем бесконечное множество, то и система (6) будет иметь бесконечное множество решений.

Решение Х = (х1, х2, …, хn) системы (6) называется допустимым, если оно содержит лишь неотрицательные компоненты, т.е. Хj >=0 для любых j = 1, 2, …, n. В противном случае решение называется недопустимым.

Среди бесконечного множества решений системы выделяют базисные решения.

Базисным решением (БР) системы m линейных уравнений с n переменными называют решение, в котором все n – m неосновных переменных равны нулю.

В задачах ЛП особый интерес представляют допустимые базисные решении (ДБР), или, как их еще называют, опорные планы. Число базисных решений является конечным, т.к. оно равно числу групп основных переменных, не превосходящему 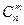. Базисное решение, в котором хотя бы одна из основных переменных равна нулю, называется вырожденным.

Пример:

В примере (7) существует три группы основных переменных, т.е. число базисных решений = 3.

Первое х1 и х2 – основные, х3 и х4 – неосновные (= 0), тогда

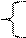х1 – х2 = 0

2х1 + х2 = 2

откуда х1 =2/3; х2 = 2/3. следовательно первое баз решение системы Х1 = (2/3; 2/3; 0; 0) –допустимое.

Если взять за основные переменные Х1 и Х3, то получим второе баз решение системы Х2 = (2/3; 0; 2/3; 0) – также допустимое. Аналогично можно найти третье баз решение при основных переменных х1, х4 Х3 = (2/3; 0; 0; -2/3) – недопустимое.

Вывод: Совместная система (6) имеет бесконечно много решений, из них базисных решений – конечное число, не превосходящее .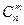

Дата добавления: 2014-01-15