Опр. Точки локальных min и max наз. точками локальных экстремумовф-ции

Экстремумы функции 2-х переменных

Опр Точка наз. точкой локального max (min) функции 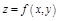, если : выполнено неравенство.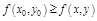

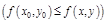Т.8. (Необходимое условие экстремума) Если функция 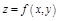достигает в точке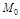локального экстремума и имеет в этой точке частные производные 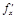, 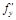то .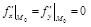

Д-во. Зафиксируем 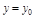. Тогда 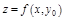– функция 1-й переменной. 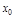– точка экстремума, следовательно,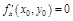. Аналогично доказываем, что.

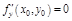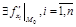Зам ечание. Для : если – точка локального экстремума ф-ции и , то .

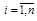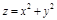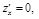
ПР. , , – точка локального min.

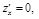
ПР. , , – нет экстремума (седло).

Опр. Точки наз. стационарными.

Пусть 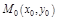– стационарная точка функции 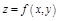и функция имеет 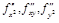в этой точке. Обозначим: , , , .

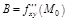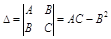Т.9. (Достаточные условия экстремума) Пусть 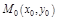– стационарная точка функции 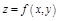и функция имеет в окрестности этой точки непрерывные частные производные до 2-го порядка включительно. Тогда:

1) если , то – то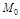чка локального max;

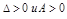, то – то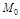чка локального min;

2) если 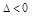, то в 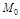нет локального экстремума.

Замечание. Если 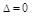, то требуется дополнительное исследование.

ПР ,

1) .

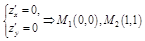2) .

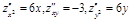– в 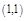-т. лок. min.

.

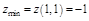§ 11. Наибольшее и наименьшее значения функции
в замкнутой области

Постановка задачи: найти 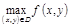, , 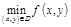где 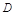– некоторая замкнутая обл-ть.

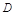– замкнутая, следовательно, ей принадлежат все ее граничные точки. Для граница 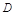– непрерывная линия.

Схема решения задачи:

1) найти стационарные точки функции 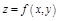: из них выбрать те, которые ;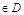

2) исследовать границы области. Т.е., если граница имеет уравнение , , то подставить в функцию 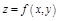: 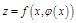; исследовать ее, как функцию 1-ой переменной при 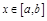. Для этого найти точки + + .

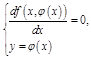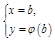3) во всех точках, полученных в 1) и 2) вычислить значения функции 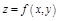. Из полученных значений выбрать наибольшее и наименьшее.

ПР. ; .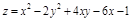

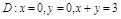1) ;

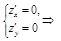
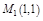2) исследуем границы:

a) : , ;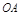

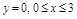
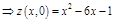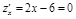
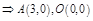b) : , ;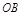

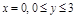
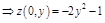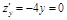
c) .

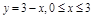
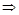
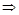
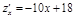
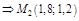3) ; ;

;

;

.

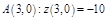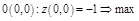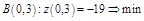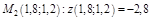§ 12. Условный экстремум

Постановка задачи: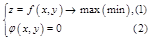

Имеем задачу оптимизации функции 1 переменной. Необходимым условием экстремума является .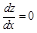

Дифференцируем (1): (3)

Дифференцируем (2): 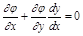(4)

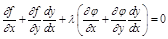: или , 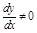для определенности.

Подберем так, чтобы 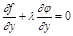. Получим:

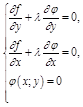(5)

Очевидно, что (5) – частные производные функции , которая наз. функцией Лагранжа,
– множитель Лагранжа.

В задача: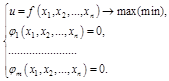

Функция Лагранжа: .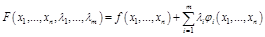

Составляем систему: все частные производные по всем переменным приравниваем 0, находим все стационарные точки. Вопрос о наличии экстремума в стационарной точке решают, как правило, на основании физического или геометрического условий задачи.

ПР. Найти прямой параллелепипед максимального объема при заданной площади поверхности .

, ,+

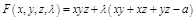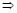
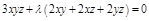
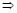
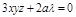
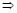
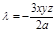
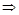
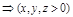
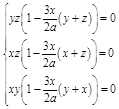
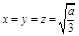, – точка max из геометрических соображений.

Дата добавления: 2014-01-15