Локальная и интегральная теоремы Муавра-Лапласа. Предельные теоремы в схеме Бернулли

Предельные теоремы в схеме Бернулли.

Лекция 7.

Увеличить изображение

Рис. 7.18. Настройка положения абзаца на странице

Установка флажка запрет висячих строк запрещает такое разделение абзаца при переходе к новой странице, при котором первая строка абзаца остается на одной странице, а вся остальная часть абзаца переходит на новую страницу. В этом случае на новую страницу будет перенесен весь абзац. Запрещается и такое разделение абзаца, при котором на новую страницу переходит только последняя строка. В этом случае на новую страницу перейдут последняя и предпоследняя строки абзаца. Такой режим разделения абзацев обычно устанавливают для всего текста документа.

Установка флажка не отрывать от следующего обеспечивает размещение абзаца всегда на той же странице, что и следующий за ним абзац. Применяют этот режим для любых заголовков и названий: при этом исключаются случаи, при которых заголовок находится на одной странице, а следующий за ним текст - на следующей.

Флажок не разрывать абзац запрещает всякое разделение абзаца между страницами. Применяют такой режим нечасто.

Флажок с новой страницы устанавливают для крупных заголовков (главы, разделы и т. п.). При этом независимо ни от чего, указанный абзац всегда будет находиться наверху страницы.

Пусть случайная величина распределена по биномиальному закону. Эта случайная величина представляет собой число успехов в серии из 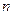испытаний, в каждом из которых может появиться успех с вероятностью или неуспех с вероятностью .Вероятность того, что в серии из 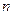испытаний появится успехов равна

, (1)

при этом , .

При больших значениях 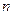и вычисление вероятности по формуле (1) представляет значительные трудности. Например, если , , 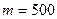, то

и вычислить такую вероятность достаточно сложно.

,Однако при выполнении определенных условий функция биномиального распределения имеет вид функции нормального распределения или функции Пуассона.

Пусть 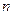достаточно велико, а не мало, так что (). Введем обозначение

. (2)

Если при величина 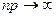, но при этом остается ограниченной величина 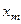, т.е. 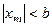, то вероятность того, что в серии из 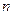испытаний будет успехов равна

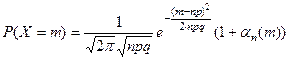, (3)

где .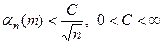

При достаточно больших 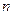эту вероятность можно выразить через функцию

Гаусса :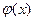

(3)

где 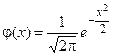, а аргумент .

Доказательство.

Для случайной величины, распределенной по биномиальному закону, вероятность появления успехов в серии из 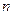испытаний равна

Учитывая, что

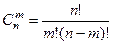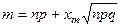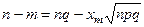, , , получим

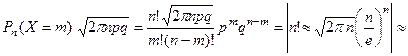
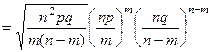(4)

При получении этого выражения была использована формула Стирлинга , справедливая при достаточно больших значениях .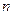

В формуле (4)

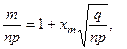при этом (5)

при этом 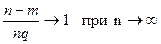(6)

при . (7)

Введем . Тогда (8)

С учетом равенств (5) и (6) получим

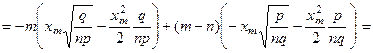
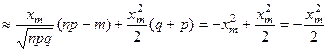(9)

При выводе этой формулы было учтено, что и. 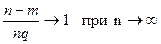, что следует из (5) и (6).

Из (9) следует, что 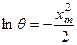, а значит 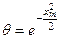. Подставляя это выражение в (8) и учитывая (5) и (6), получим

(10)

, где .

Из теоремы Муавра-Лапласа следует, что при больших значениях 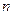и не малых значениях функция биномиального распределения имеет вид функции нормированного нормального распределения с 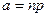и .

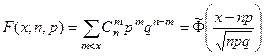, (11)

где

Дата добавления: 2014-01-15