Неравенство Чебышева. Известно, что нельзя заранее предвидеть, какое из возможных значений примет случайная величина в итоге эксперимента

Закон больших чисел

Известно, что нельзя заранее предвидеть, какое из возможных значений примет случайная величина в итоге эксперимента, но при очень большом числе случайных явлений их результат практически перестает быть случайным и может быть предсказан с большой степенью определенности.

Особенности случайного явления не оказывают влияния на средние результаты большого числа испытаний (эти особенности взаимно погашаются). Частота появления события, среднее арифметическое и статистическая дисперсия обладают удивительной устойчивостью при большом числе испытаний. Поэтому становится возможным предсказание средних результатов случайных явлений почти с полной достоверностью.

Для практики очень важно знание условий, при выполнении которых совокупное действие случайных причин приводит к результату, почти не зависящему от случая. Эти условия и указываются в теоремах и неравенствах, носящих общее название закона больших чисел.

Для любой случайной величины (дискретной или непрерывной, распределенной по любому закону с математическим ожиданием и дисперсией 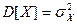для любого вещественного числа справедливо неравенство

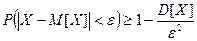. (21)

Или 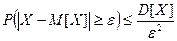(22)

Доказательство.

Докажем справедливость неравенства (21) для непрерывной случайной величины. Из определения вероятности

=

Отсюда 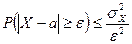и следовательно, .

Неравенство Чебышева (22) не позволяет найти вероятность случайной величине отклониться по абсолютной величине от своего математического ожидания на величину, большую , а устанавливает лишь для нее верхнюю границу. Например, для нормально распределенной случайной величины в соответствии с правилом . Неравенство Чебышева дает следующую верхнюю границу .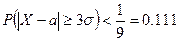

Следствие из неравенства Чебышева.

Если , то почти достоверно, что случайная величина равна своему математическому ожиданию.

Дата добавления: 2014-01-15