Частотное представление стационарных случайных сигналов

Наборы инструкций AES

Расширение системы команд AES (Advanced Encryption Standard) — расширение системы команд x86 для микропроцессоров, предложенное компанией Intel в марте 2008. Целью данного расширения является ускорение приложений, использующий шифрование и дешифрование по алгоритму AES. Сходное расширение PadLock engine существует в микропроцессорах от VIA Technologies.

Контрольные вопросы

1. Перечислите основные типы наборов инструкций, применяемых в ЭВМ.
2. Какие наборы инструкций используются при работе с графикой?
3. Какие инструкции использованы для шифрования данных?
4. Типы логических команд.
5. Охарактеризуйте команды переходов.

Дискретные спектры.

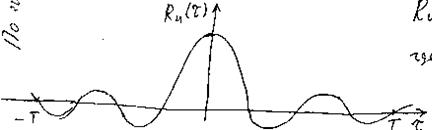
Корреляционную функцию R _u(t) (см. рис. 15) стационарного случайного процесса, заданного на конечном интервале времени [- T, T ], можно разложить в ряд Фурье (15), условно считая ее периодически продолжающейся с периодом 4 Т (при – T < t ₁, t ₂ < T, -2 T < t <2 T):

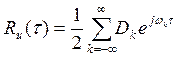(91)

где w _k = k w ₁, w ₁= p / 2 T;

По аналогии с (64)

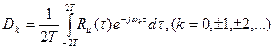(92)

Учитывая, что R _u(t) является четной функцией, имеем

(93)

Положив t = t ₁ – t ₂, находим

(94)

что согласно (89) представляет собой каноническое разложение корреляционной функции. По нему, как было указано ранее, получаем разложение случайного процесса:

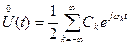, (95)

причем

(96)

Выражение (95) записано для случайного процесса с нулевой постоянной составляющей, что характерно для многих реальных сигналов. В общем случае в правую часть этого выражения необходимо добавить постоянную величину, соответствующую математическому ожиданию случайного процесса (m _u). Корреляционная функция при этом не изменяется.

Очевидно, что при попарном объединении экспоненциальных составляющих с одинаковыми положительными и отрицательными индексами k каноническое разложение (95) приводится к тригонометрической форме.

Таким образом стационарный случайный процесс на ограниченном интервале времени можно представить совокупностью гармонических составляющих различных частот с амплитудами, являющимися некоррелированными случайными величинами, математические ожидания которых равны нулю.

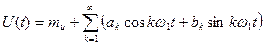(96 а)

где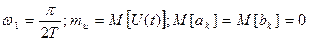

На спектральной диаграмме такого процесса каждой гармонике ставится в соответствие вертикальный отрезок длина которого пропорциональна дисперсии ее амплитуды, а расстояние на оси абсцисс отвечает частоте. (рис. 16)

Рис. 16

Чтобы получить описание стационарного случайного процесса в точном смысле, т.е. справедливое для любого момента времени на бесконечном интервале -¥<t<¥ необходимо перейти к интегральному каноническому разложению.

Дата добавления: 2014-01-15