ЛЕКЦИЯ 8. Интегральное каноническое разложение для корреляционной функции получим из формулы (91) путем предельного перехода при Т®¥

Непрерывные спектры.

Интегральное каноническое разложение для корреляционной функции получим из формулы (91) путем предельного перехода при Т®¥. Увеличения интервала времени, на котором наблюдается случайный процесс, сопровождающийся уменьшением значений дисперсий, что следует из (92), а также сокращением расстояний между спектральными линиями, поскольку

(97)

При достаточно большом, но конечном Т можно записать выражение для средней плотности распределения дисперсии по частоте:

(98)

где 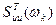- средняя плотность дисперсии на участке, прилегающем к частоте w_k

Теперь можно преобразовать формулы (91) и (98) к виду. D_k подставляем из (92).

(99)

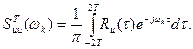(100)

Переходя к пределу при Т®¥, получаем

(101)

где

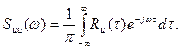(102)

Т.к. величина 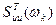D w являлась не только дисперсией D _k коэффициента разложения корреляционной функции R _u(t), но и дисперсией D [ C _k] коэффициента разложения случайного процесса U (t), то величина S _uu(w)d w, полученная в результате предельного перехода при Т ®¥, представляет собой дисперсию, приходящуюся на спектральные составляющие стационарного случайного процесса, занимающие бесконечно малый интервал частот (w, w +d w). Функцию S _uu(w), характеризующую распределения дисперсии случайного процесса по частотам, называют спектральной плотностью стационарного случайного процесса U ( t ).

Выражение для интегрального канонического разложения корреляционной функции R _u(t) найдем, положив в формуле (101) t = t ₁ – t ₂ :

(103)

Обозначив и повторив процедуру предельного перехода при Т ®¥ для соотношения (95), получим каноническое разложение стационарной случайной функции :

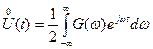(104)

где дисперсией случайной функции G (w)d w является функция S _uu(w)d w.

Основные свойства спектральной плотности.

Поскольку понятие спектральной плотности стационарно случайного процесса играет большую роль при исследовании преобразования сигналов линейными системами, уточним ее свойства и физический смысл.

Отметим, что в формулах (101) и (102) S _uu(w) определима как для положительных, так и для отрицательных частот. Перейдем к одностороннему спектру, ограничиваясь только положительными частотами. Воспользовавшись формулой Эйлера, представим соотношение (102), состоящим из двух слагаемых

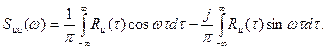
В силу частности функции R _u(t) второе слагаемое равно нулю, а первое можно преобразовать к виду

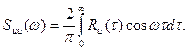(105)

Из (105) следует, что S _uu(w) является действительной и четной функцией, т.е.

S _uu(w) = S _uu(- w) (106)

Это позволяет ограничиться положительными частотами и в (101):

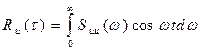(107)

Соотношения (101) и (102), а также (105) и (107) являются парами интегрального преобразования Фурье, причем (105) и (107) для случая четной функции. Поэтому корреляционная функция и спектральная плотность подчинены закономерности: чем протяженнее кривая S _uu(w), тем уже корреляционная функция R _u(t) (тем меньше время корреляции) и наоборот.

Площадь ограниченная непрерывной кривой S _uu(w) по спектральной диаграмме, очевидно должна равняться дисперсии D _u случайного процесса U (t). Действительно, положив в формуле (107) t = 0, получим

(108)

Подразумевая под случайным процессом U (t) напряжение, D _u можно рассматривать как среднюю мощность, выделяемую этим напряжением на резисторе с сопротивлением в 1 Ом:

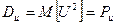(109)

следовательно, величина

(110)

представляет собой долю средней мощности, выделяемой составляющими спектра, относящимися к интервалу частот (w, w + d w).

В связи с этим спектральную плотность S _uu(w) называют еще спектральной плотностью мощности, а также энергетическим спектром стационарного случайного процесса, поскольку S _uu(w) имеет размерность энергии.

Спектральная плотность мощности случайного процесса является средней характеристикой множества реализаций. Ее можно получить и путем усреднения спектральной плотности мощности реализации P _k(w) (62) по множеству реализаций.

Рассмотрим с этой целью одну реализацию стационарного случайного процесса U(t) сначала на ограниченном интервале времени –Т<t<T. Для нее можно записать преобразование Фурье:

(111)

В соответствии с (63) спектральная плотность мощности этой реализации

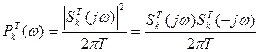(112)

Найдем среднее значение по множеству реализаций k. Имеем

или

(113)

Т.к. мы предполагаем, что случайный процесс стационарный, то

(114)

где t ₁ – t ₂ = t.

При выполнении условия (114) для выражения (113) существует предел при Т ®¥:

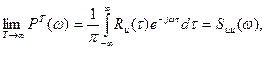(115)

что и требовалось доказать.

Дата добавления: 2014-01-15