Кратные интегралы

Лекция 8.

Мера Жордана. Жордановы множества.

Областью в пространстве называется непустое связное открытое множество. Замыкание области называется замкнутой областью. Замкнутым называется множество, содержащее все свои предельные точки. Замкнутое множество называется границей области .

Диаметром области 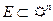называется точная верхняя грань расстояний между точками области

, где , ,.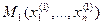

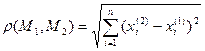Для замкнутой ограниченной области диаметр равен наибольшему из расстояний между точками области.

Стандартным прямоугольником называется прямоугольник со сторонами, параллельными координатным осям, например,

замкнутый стандартный прямоугольник

(1)

открытый стандартный прямоугольник

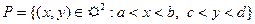, (2)

а также полуоткрытые прямоугольники, для которых хотя бы одно из трех неравенств в вышеприведенном определении (1) является строгим. Обозначим через множество стандартных прямоугольников на плоскости.

Два прямоугольника , 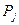называются непересекающимися, если они не имеют общих внутренних точек. Для прямоугольника , который является объединением непересекающихся стандартных прямоугольников , будем использовать специальное обозначение . Каждому прямоугольнику можно сопоставить число – его меру, которая удовлетворяет условиям неотрицательности: 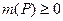и аддитивности: . В частности, мерой непустого стандартного прямоугольника (замкнутого, открытого или полуоткрытого), определяемого числами 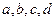, является его площадь .

Связное плоское множество называется элементарным, если его можно представить как объединение конечного числа непересекающихся стандартных прямоугольников .

Стандартным прямоугольным параллелепипедом в называется . Два параллелепипеда , называются непересекающимися, если они не имеют общих внутренних точек. Мерой или объемом стандартного параллелепипеда 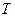называется .

Элементарным телом называется связное множество точек пространства , представляющее собой объединение конечного числа непересекающихся -мерных стандартных прямоугольных параллелепипедов. Мера или объем элементарного тела 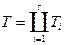равна сумме мер стандартных прямоугольных параллелепипедов .

Рассмотрим произвольную область 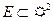на плоскости, проведем прямые, параллельные координатным осям. В результате получим стандартные прямоугольники. Обозначим такое разбиение через 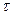. Пусть – площадь стандартных прямоугольников, лежащих внутри и не имеющих общих точек с границей области, а – площадь стандартных прямоугольников, имеющих хотя бы одну общую точку с границей области. Тогда для разных разбиений 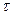получим множестваи .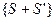

Нижней или внутренней мерой Жордана множества называется ; верхней или внешней мерой Жордана называется . Множествоназывается измеримым по Жордану, если и 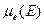конечны и 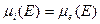. В этом случае величина 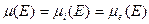называется мерой Жордана, а множество называется жордановым. Аналогичным образом определяется мера области , 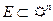. Мера Жордана обладает свойствами неотрицательности (), аддитивности () и монотонност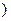и (.Если жорданово множество, то .

Множество 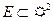, границей которого является спрямляемая (в частности кусочно-гладкая) замкнутая кривая без самопересечений является жордановым множеством. Множество , границей которого является кусочно-гладкая замкнутая поверхность без самопересечений, является жордановым множеством.

Жордановой мерой ограниченного участка кривой или отрезка является длина, жордановой мерой ограниченной замкнутой плоской области или поверхности является площадь, жордановой мерой тела в трехмерном пространстве, ограниченного замкнутой поверхностью, является объем.

Дата добавления: 2014-01-15