Интеграл Римана по измеримому по Жордану множеству и его свойства

Пусть 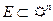– жорданово множество, на котором задана ограниченная функция . Разбиением множества 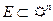называется конечная система непустых непересекающихся жордановых множеств , объединение которых равно заданному множеству: . Диаметром разбиения 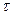называется . Выберем произвольно точки , и составим интегральную сумму Римана

(3)

Интегралом Римана от функции по измеримому по Жордану множеству называется число

, (4)

которое не зависит ни от способа разбиения множества , ни от выбора точек . Для интеграла Римана используется также следующее обозначение

.

Такой интеграл называется кратным интегралом.

Если 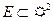– плоская область, жордановой мерой которой является площадь, то =– двойной интеграл. Если – область в трехмерном пространстве, жордановой мерой которой является объем, то =– тройной интеграл.

Множество интегрируемых по Риману функций на множестве обозначается R.

Если Rи , то ограничена на .

Если измеримое по Жордану замкнутое ограниченное множество и , то R.

Если измеримое по Жордану замкнутое ограниченное множество, ограничена на и множество точек разрыва функции имеет жорданову меру нуль, то R. В частности, ограниченная функция, имеющая не более чем счетное множество точек разрыва на жордановом множестве , интегрируема по Риману на этом множестве.

Основные свойства кратного интеграла Римана

Будем считать в дальнейшем множества измеримыми по Жордану и функции ограниченными на рассматриваемых множествах.

1. .

2. R, RRдля любых постоянных и и (свойство линейности интеграла).

3. R, R,

Rи (свойство аддитивности интеграла). Отметим, что здесь существенным условием является ограниченность функции на множествах и .

4. R, RRи R, если .

5. Если R, Rи для любых , то . В частности, если Rи для любых , то .

6. Если R, , , то

.

7. Если R, , , R, для любых , то .

8. Если ограничена на , Rи почти везде на (т.е. равенство нарушается на множестве меры нуль), то .

Сведение кратных интегралов к повторным интегралам

Для вычисления двойных и тройных интегралов необходимо свести их к повторным интегралам. Это можно сделать на основе теоремы Фубини.

Область , где , , называется стандартной относительно оси , если любая прямая, параллельная оси , пересекает границу этой области не более, чем в двух точках. Иногда такая область называется правильной в направлении оси . Аналогично определяются область на плоскости, стандартная относительно оси (правильная в направлении оси ):

, где , . Стандартная относительно координатной оси область и ее замыкание являются жордановыми множествами.

Теорема Фубини для стандартной плоской области.

Если , где, , и , то

. (5)

Если , где , и , то

. (6)

Замечание. При практическом использовании формул необходимо, чтобы , (соответственно , ), в противном случае представляют интеграл в виде суммы интегралов.

Теорема Фубини для правильной пространственной области.

Пусть ограниченная и замкнутая пространственная область, правильная в направлении оси , т.е. любая прямая, параллельная оси, пересекает границу области не более чем в двух точках. Тогда – измеримый компакт. Если

, ,

, , , то

. (7)

Аналогично формулируется теорема Фубини для пространственной области, правильной в направлении оси : если

, , ,

, , , то

. (8)

Теорема Фубини для пространственной области, правильной в направлении оси : если , , ,

, , , то

. (9)

Теорема Фубини для правильной области в .

Пусть – измеримый по Жордану компакт в .

…,

. Функции , …,, непрерывны в области определения (например, функции , непрерывны на – измеримом по Жордану компакте), функция . Тогда

(10)

Пример 1. Вычислить интеграл , где – область, ограниченная прямыми , и гиперболой .

Найдем точки пересечения кривых, ограничивающих заданную область, решив соответствующие системы уравнений

.

Отсюда следует, что область может быть представлена в виде . Тогда интеграл равен

Область можно представить также в виде , где ,

.и тогда интеграл представляет собой сумму двух интегралов

Пример 2. Вычислить тройным интегрированием объем тела , ограниченного цилиндрами , и плоскостями , .

Объем тела определяется тройным интегралом . Сведем тройной интеграл к трехкратному.

Здесь видны две цилиндрические поверхности, которые ограничивают тело снизу и сверху и две плоскости. Построим тело, объем которого нужно найти.

Спроектируем тело на плоскость . В результате получится прямоугольник, две стороны которого лежат на прямых с уравнениями , . Найдем уравнения прямых, на которых лежат две другие стороны прямоугольника. Для этого исключим из уравнений цилиндров переменную и решим полученное уравнение

.

Отсюда тело , объем которого нужно найти, можно представить в виде .

Полученные неравенства определяют пределы интегрирования в повторном интеграле, к которому сводится тройной интеграл

Следовательно, объем тела равен 8.

Дата добавления: 2014-01-15