Поиск допустимого базиса

Свойства алгоритмов симплекс-таблиц

ЛЕКЦИЯ № 8

1) Для случая невырожденных базисных допустимых решений (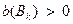) алгоритмы симплекс-таблиц обладают свойствами полноты, определенности, сходимости к оптимальному решению за конечное число итераций.

2) При решении вырожденных задач (когда одна или несколько базисных компонент на ряде итераций алгоритма оказываются равными нулю) появляется возможность зацикливания алгоритма. Такая возможность определяется тем, что при вырожденных базисных решениях шаг перемещения от одного базисного решения к другому оказывается нулевым (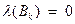). Алгоритм как бы "топчется" на одном месте, оставаясь в одной и той же крайней точке: происходит лишь формальная замена базисных компонент. Теряется целенаправленность перебора базисных решений, так как 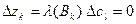, и может реализоваться следующий случай:

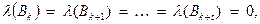
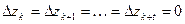,причем .

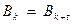Необходимо сказать, что в большинстве случаев при решении практических задач алгоритмы симплекс-таблиц работают с вырожденными базисными решениями, но при этом, как правило, если не брать в расчет специально сконструированные примеры, зацикливания не происходит. Однако принципиальная возможность зацикливания заставила разработать различные методы выхода из такой ситуации. Сущность методов состоит в более сложной процедуре выбора разрешающей строки, чем правило (1.64), когда 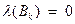и возникает неоднозначность выбора.

Наиболее простой и часто применяемой процедурой является использование псевдослучайного механизма выбора разрешающей строки из тех, для которых 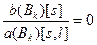. При этом вероятность многократного повторения цикла сводится к нулю.

3) Алгоритмы симплекс-таблиц, реализуемые на ЭВМ, из-за ее ограниченной разрядной сетки обладают свойством накопления ошибок вычислений при выполнении преобразований Гаусса-Жордана. При этом проблема не в том, что в результате будет получено приближенное оптимальное решение ЗЛП, а в том, что могут возникнуть условия для сбоя в работе алгоритма. Это может произойти при выполнении операций сравнения чисел с нулем: при проверке условия оптимальности и выборе разрешающего столбца, при проверке условия 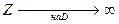и выборе разрешающей строки, - когда вместо действительного нулевого значения рассматриваемого элемента симплекс-таблицы в ЭВМ будет определено очень малое положительное число (погрешность вычисления). Принципиально возможны два подхода к решению этой проблемы.

Первый подход состоит в переходе от работы с действительными числами к работе с рациональными дробями. Но он имеет свой недостаток: аварийное завершение работы алгоритма может произойти из-за переполнения разрядной сетки ЭВМ при вычислении целых значений числителей или знаменателей рациональных дробей.

Второй подход состоит в оценке накопившейся погрешности и проверке необходимых условий с учетом этой погрешности.

4) Вычислительная сложность нахождения оптимального решения ЗЛП алгоритмами симплекс-таблиц определяется с точностью до константы следующим произведением:

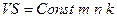, (1.91)

где m, n – соответственно число ограничений и число переменных ЗЛП;

k – число итераций алгоритма.

Основная проблема использования (1.91) для расчета объема проводимых вычислений состоит в оценке k. Для большинства реальных задач k редко превосходит более чем несколько раз m и n. Эффективно решаются практические задачи с тысячами переменных и ограничений. Однако отсутствует доказательство, что вычислительная сложность решения ЗЛП симплекс-методом растет полиномиально с ростом m и n. Более того, были сконструированы ЗЛП очень простой структуры, на решение которых алгоритм затрачивает экспоненциально большое число шагов:

.

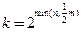При столкновении с такой задачей размерности 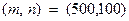симплекс метод порождает последовательность из 10¹⁸ арифметических операций [ ], на выполнение которых компьютеру с быстродействием 1 млрд. оп/сек потребовалось бы несколько десятков лет.

В последние годы показано, что возможно построение для решения таких задач алгоритмов, принципиально отличных от симплекс-метода и имеющих полиномиальную сложность от битовой размерности ЗЛП (m, n, е), где е – число разрядов ЭВМ, используемых для хранения результатов вычисления (метод эллипсоидов, метод Кармаркара). Для обычных же задач применение этих методов намного менее эффективно, чем использование симплекс-метода.

Очевидный допустимый базис для ЗЛП может быть сформирован лишь в некоторых частных случаях.

Наиболее типичным и часто реализуемым случаем является решение ЗЛП, формализованная постановка которых имеет стандартную форму с положительным вектором правых частей ограничений. Это, как правило, задачи типа распределения ресурсов (см. пример "Производственная задача", раздел 1.1.1). После перехода к канонической форме путем введения балансовых переменных базис, составленный из столбцов при этих переменных, является очевидным допустимым. При этом базисная матрица – единичная. Поэтому легко формируется начальная симплекс-таблица для поиска оптимального решения таких ЗЛП.

В общем же случае нахождение допустимого базиса является самостоятельной задачей. Ниже рассматривается метод минимизации невязок, использующий для своей реализации алгоритмы симплекс-таблиц поиска оптимального решения ЗЛП. Эти алгоритмы применяются к вспомогательной ЗЛП, специальным образом формируемой, имеющей очевидный начальный допустимый базис и по результатам решения которой можно найти допустимый базис исходной ЗЛП или сделать вывод о пустоте множества допустимых решений последней.

Дата добавления: 2014-01-15