Метод минимизации невязок

Приведем исходную ЗЛП к канонической форме с неотрицательными значениями правых частей ограничений. Таким образом, основные ограничения будут иметь вид:

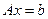, где 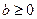. (1.92)

Введем в каждое i -ое ограничение соответствующую фиктивную переменную, присвоив ей номер (n + i):

, .

В матричной форме основные ограничения примут вид:

, (1.93)

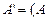где Е);

- единичная матрица размерности m´m.

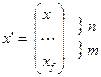- вектор размерности n+m.

В системе уравнений (1.93) базис, составленный из столбцов матрицы Е (столбцов при фиктивных переменных), является очевидным допустимым базисом. Очевидным также является утверждение, что множество допустимых базисных решений основных ограничений исходной задачи (1.92), если оно не пусто, является подмножеством базисных допустимых решений (1.93).

Выше рассмотрена процедура последовательного перебора допустимых базисных решений ЗЛП. Для ее использования при решении задачи перехода от известного допустимого базиса (1.93) к допустимому базису (1.92) необходимо придать ей целенаправленный характер: цель – замена начального множества базисных столбцов при фиктивных переменных базисными столбцами при переменных исходной задачи. Такой цели будет соответствовать решение следующей ЗЛП, которую назовем вспомогательной задачей:

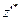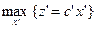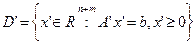=, , (1.94)

где в дополнение к (1.93)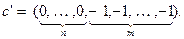

Начальное базисное множество этой ЗЛП, определяющее ее очевидное допустимое базисное решение, .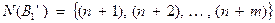

При направлении оптимизации на max задание коэффициентов целевой функции при фиктивных переменных отрицательными числами (для простоты и определенности "-1") определит работу алгоритма поиска оптимального решения задачи (1.94) таким образом, что он будет стремиться обнулить фиктивные переменные, то есть вывести их из базиса (в самом начале решения (1.94) их значения равны соответствующим компонентам вектора b).

По результатам решения вспомогательной задачи (1.94) можно сделать следующие выводы относительно допустимого базисного решения исходной задачи:

1) Если в оптимальном решении вспомогательной задачи (1.94) 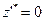, то 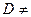Æ. (этому соответствует, как правило, случай, когда все фиктивные переменные выведены из базисного множества; если же некоторые из них остались базисными, то, очевидно, они имеют нулевые значения и с помощью дополнительных процедур преобразований Гаусса-Жордана могут без проблем переведены в состав небазисных путем замены их в базисном множестве небазисными переменными исходной задачи). В этом случае заключительный базис вспомогательной задачи (после дополнительного вывода из базисного множества оставшихся там фиктивных переменных) является допустимым базисом исходной ЗЛП 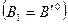. С него можно начать работу алгоритма поиска оптимального решения исходной задачи.

2) В противном случае (этому соответствует 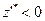) можно сделать вывод о том, что множество допустимых решений исходной ЗЛП является пустым .

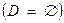Дата добавления: 2014-01-15