Первый критерий продуктивности. Матрица A продукти­вна тогда и только тогда, когда матрица сущест­вует и ее элементы неотрицательны

Теорема 9.1. Если для матрицы A с неотрицательными элементами и некоторого вектора с неотрицательными компонентами уравнение (9.1) имеет решение с неотри­цательными компонентами, то матрица A продуктивна.

Иными словами, достаточно установить наличие положи­тельного решения системы (9.1) хотя бы для одного положи­тельного вектора , чтобы матрица A была продуктивной.

Пе­репишем систему (9.1) с использованием единичной матрицы E в виде

(Е – А)= . (9.2)

Если существует обратная матрица , то существует и единственное решение уравнения (9.2):

= . (9.3)

Матрица называется матрицей полных затрат.

Существует несколько критериев продуктивности матри­цы A. Приведем два из них.

Второйкритерий продуктивности. Матрица A с неотри­цательными элементами продуктивна, если сумма элемен­тов по любому ее столбцу (строке) не превосходит единицы: , причем хотя бы для одного столбца (строки) эта сумма строго меньше единицы.

Рассмотрим применение модели Леонтьева на примерах.

Пример 1. В табл. 9.1 приведены данные по балансу за не­который период времени между пятью отраслями промышлен­ности. Найти векторы конечного потребления и валового вы­пуска, а также матрицу коэффициентов прямых затрат и опре­делить, является ли она продуктивной в соответствии с при­веденными выше критериями.

Таблица 9.1

№	Отрасль	Потребление	Конечный продукт	Валовый выпуск у.д.е.
	Станкостроение Энергетика Машиностроение Автомоб. промышленн. Добыча и переработка углеводородов	15 12 24 23 16 10 3 35 15 7 10 5 10 10 10 0 5 10 5 5   7 15 15 10 3

Решение. В данной таблице приведены составляющие ба­ланса в соответствии с соотношениями (11.8): — первые пять столбцов, 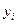— шестой столбец, - последний столбец (i,j = 1,2,3,4,5). Вычислив по формулам (11.9) и (11.10), имеем

, ,

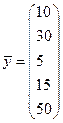Все элементы матрицы A положительны, однако нетрудно видеть, что их сумма в третьем и четвертом столбцах боль­ше единицы. Следовательно, условия второго критерия продук­тивности не соблюдены и матрица A не является продуктив­ной. Экономическая причина этой непродуктивности заключа­ется в том, что внутреннее потребление отраслей 3 и 4 слиш­ком велико в соотношении с их валовыми выпусками.

Пример 2. Табл. 9.2 содержит данные баланса трех отрас­лей промышленности за некоторый период времени. Требуется найти объем валового выпуска каждого вида продукции, если конечное потребление по отраслям увеличить соответственно до 60, 70 и 30 условных денежных единиц.

Таблица 9.2

№	Отрасль	Потребление	Конечный продукт	Валовый выпуск
	Добыча и переработка углеводородов Энергетика Машиностроение

Решение. Выпишем векторы валового выпуска и конеч­ного потребления и матрицу коэффициентов прямых затрат. Согласно формулам (**) и (9,1), имеем

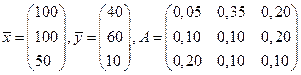
Матрица A удовлетворяет обоим критериям продуктивности. В случае заданного увеличения конечного потребления новый вектор конечного продукта будет иметь вид

(9.4)

Требуется найти новый вектор валового выпуска 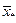, удов­летворяющий соотношениям баланса в предположении, что матрица A не изменяется. В таком случае компоненты неизвестного вектора 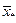находятся из системы уравнений, которая имеет в данном случае вид

В матричной форме эта система выглядит следующим об­разом:

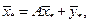или (E-A), (9.5)

где матрица (Е - А) имеет вид

(Е - А) =

Решение системы линейных уравнений при заданном векторе правой части (например, методом Гаусса) да­ет новый вектор 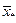как решение системы уравнений баланса (9.5):

Таким образом, для того чтобы обеспечить заданное уве­личение компонент вектора конечного продукта, необходимо увеличить соответствующие валовые выпуски: добычу и переработку углеводородов на 52,2%, уровень энергетики на 35,8% и выпуск продукции машиностроения - на 85% по срав­нению с исходными величинами, указанными в табл. 9.2

Дата добавления: 2014-01-15