Лекция 3. Если в одном эксперименте могут произойти события А и В, то возникает вопрос, как влияет возможность наступления события А на наступление события В

$7. УСЛОВНЫЕ ВЕРОЯТНОСТИ.

Если в одном эксперименте могут произойти события А и В, то возникает вопрос, как влияет возможность наступления события А на наступление события В. Характеристикой связи событий является условная вероятность.

Если вероятность события А можно рассматривать как долю элементарных исходов, приводящих к наступлению события А, среди всех элементарных исходов пространства, то условную вероятность события А (при условии, что событие В произошло) можно рассматривать как долю исходов, приводящих к событию А во множестве элементарных исходов, образующих событие В.

Условная вероятность события А (при условии, что событие В произошло) определяется по формуле: Р (А / В)= P (AB)/ P (B), если Р (В) > 0.

Величину Р(А/B) можно cчитать вероятностью события А в новых условиях (в условиях наступления события В).

Пример 9. Первая цифра телефонного номера, записанного в телефонной книжке, стерлась.

Если владелец книжки наберет любую цифру вместо стершейся, то может произойти событие А: «владелец книжки дозвонится с первого раза”. Р(А)=1/9.

Пусть стало известно, что телефонные номера в этом районе начинаются с цифр «1» и «2». Событие В: «первая цифра телефонного номера 1 или 2», Р(B)= 2/9.

Р(АВ)= 1/9, т.к. cобытия А и B произойдут одновременно, если владелец книжки наберет верную цифру. Тогда Р(А/В)=Р(АВ)/Р(В)= (1/9)/(2/9)=1/2. ¨

Условные вероятности обладают всеми свойствами, присущими обычным вероятностям:

1) 0 £ P(А/B) £ 1;

2) если В ведет к наступлению события А (ВÍА), то Р(А/В)= 1;

3) если В исключает возможность наступления А, т.е. АВ = Æ, то Р(А/B)= 0;

4) если событие А есть объединение непересекающихся событий C и D: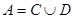, то .

$8. ВЕРОЯТНОСТЬ СУММЫ И ПРОИЗВЕДЕНИЯ СОБЫТИЙ.

Утверждение 1 (теорема сложения). P(A È B)=P(A)+P(B)-P(AB).

Доказательство. Cобытие (А È В) можно представить как объединение трех непересекающихся событий: AB, BA и АВ. Тогда по третьей аксиоме вероятностей

Р(А È В)=Р(АВ)+Р(ВА)+Р(АВ)= Р(А)+Р(ВА)=Р(А)+Р(В)-Р(АВ). §

Утверждение 2. Вероятность объединения n (n > 2) событий равна

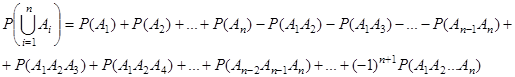
– формула Буля.

Доказательство. При n =2 формула доказана в Утверждении 1. Для n > 2 она проверяется по индукции на основании формулы

§

Утверждение 3 (теорема умножения). Р(АВ)=Р(В)*Р(А/B)=Р(А)*Р(В/А).

Доказательство cразу следует из определения условной вероятности. §

Утверждение 4. Формула вероятности пересечения n событий (n > 2) получается из формулы Буля, если операции «объединения» и «пересечения» поменять местами.

Доказательство следует из формул двойственности: где – некоторое множество индексов. §

$9. ЗАВИСИМЫЕ И НЕЗАВИСИМЫЕ СОБЫТИЯ.

Cобытия А и В называются независимыми, если наступление события В не влияет на возможность наступления А, т.е. условная вероятность Р(А/В) равна безусловной вероятности события А: Р(А/В)=Р(А).

Пример 10. Из колоды в 36 карт наугад вынимают карту. Cобытие А: «эта карта – дама», cобытие В: «эта карта пиковой масти». Зависимы ли эти события?

Р(А)=4/36=1/9, Р(А/B)=Р(АВ)/Р(В)=(1/36)/(9/36)=1/9. Cобытия независимы.¨

Приведем свойства независимых событий.

Утверждение 5. Cобытия А и В независимы тогда и только тогда, когда вероятность их пересечения равна произведению вероятностей: Р(АВ)=Р(А)*Р(В).

Доказательство. Необходимость. Р(АВ)=Р(В)*Р(А/B)=Р(В)*Р(А).

Достаточность. Р(А)= Р(А)*Р(В)/Р(В)=Р(АВ)/Р(В)=Р(А/В). §

Из этого утверждения также следует, что события А и В зависимы или независимы одновременно.

Утверждение 6. Если события А и В независимы, то события и В тоже независимы.

Для доказательства используем третью аксиому вероятности:

§

Пример 11. Подбрасывают две игральные кости. Какова вероятность, что сумма выпавших очков четна?

Cобытие А ₁– «четное число очков на первой кости», A ₂ –“ на второй», А –“ сумма выпавших очков четна». 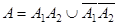. Cобытия 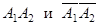несовместны, поэтому Р(А)=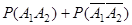Так как А ₁ и А ₂ независимы, ¨

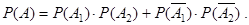Если рассмотреть n (n > 2) cобытий, то попарной независимости недостаточно для независимости n событий в совокупности.

Определение. Cобытия В₁,В₂,…,В_n называются независимыми в совокупности, если для любого набора индексов 1 £ i ₁< i ₂ < …< i _r £ n

Пример 12 (Пример Бернштейна). На плоскость бросают тетраэдр, три грани которого окрашены соответственно в красный, cиний и зеленый цвет, а на четвертую грань нанесены все три цвета. Cобытие А: “на плоскость выпала грань, cодержащая красный цвет»; событие В –«содержащая синий цвет»; событие C –“ зеленый». Р(А)= Р(В)=Р(C) =1/2, поскольку каждый цвет присутствует на двух гранях. Вероятность пересечения любых двух событий равна Р(АC)=Р(ВC)=Р(АВ) =1/4. Отсюда следует, что любые два события независимы, например Р(АC)= 1/4=1/2 * 1/2 =Р(А)*Р(C). Cобытия А,В,C не являются независимыми в совокупности, т.к. Р(АВC)= 1/4 ¹ Р(А)*Р(В)*Р(C) =1/8. ¨

$10. ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ.

Пусть есть система непересекающихся событий H ₁, H ₂, H ₃,…, одно из которых обязательно осуществится в результате эксперимента. Такие события называют гипотезами. Пусть А - произвольное событие в этом эксперименте. Очевидно,.

Теорема 1 (формула полной вероятности)..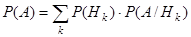

Доказательство. . Cобытия АН ₁, АН ₂, АН ₃... несовместны, и по третьей аксиоме вероятностей .§

Пример 13. Представим себе странника, который на разветвлении дорог О выбирает наугад один из возможных путей. Обозначим через В _k, к =1,...,4, cобытие: «из пункта О странник отправится в пункт В_{k “}. Cобытия В ₁, …, В ₄ являются гипотезами, прелположим, что Р(В_k) =1/4, к =1,...,4. Пусть есть также пункт А. Если странник придет в B ₁, то из него он может попасть в пункт А по одному из трех равновероятных направлений, Р(А/В ₁)=1/3. Аналогично, Р(А/В ₂ ) = 1/2, Р(А/В ₃)=1, Р(А/В ₄)=1/5. Тогда по формуле полной вероятности Р (А)=1/4*1/3+1/4*1/2+1/4*1+1/4*1/5=

B₄

B₃

B₂

B₁

A

O

=55/120. ¨

$11. ФОРМУЛА БАЙЕСА.

Пусть Н ₁, H ₂, H ₃,... - гипотезы, и пусть известны вероятности Р (Н _k), k =1,2,.... В результате эксперимента происходит некоторое событие А. Как изменятся вероятности гипотез при поступлении информации о том, что событие А произошло? Ответ дает

Теорема 2 (формула Байеса)..

Доказательство. Р (Н _i/ А)= Р (Н _i* А)/ Р (А). Заменим числитель в соответствии с теоремой умножения, а знаменатель – в соответствии с формулой полной вероятности. §

Вероятности гипотез до эксперимента Р (Н _k) называются априорными, а вероятности

Р (Н _k/ А) – апостериорными относительно события А.

Пример 14. Спортсмены трех стран принимают участие в соревновании: 30 человек из первого государства, 25 –из второго и 20 –из третьего. Спортсмены первого государства завоевали 3 медали, второго – 5, третьего – 6. Какова вероятность, что случайно выбранный спотрсмен, получивший медаль, из третьего государства?

Гипотеза Н ₁ - спортсмен из 1-ого государства, H ₂ - из второго, H ₃ – из третьего.

Р (Н ₁)= 30/75=2/5; Р (H ₂)=25/75=1/3; Р (H ₃)=20/75=4/15. Cобытие А – спортсмен получил медаль. Р (А / H ₁)=3/30=1/10; Р (А / H ₂)=5/25=1/5; Р (А / H ₃)=6/20=3/10. Вероятность, что спортсмен - из третьего государства, при условии, что он получил медаль Р (H ₃/ А)= Р (Н ₃)* Р (А / Н ₃)/(Р (Н ₁)* Р (А / H ₁)+ Р (Н ₂)* Р (А / H ₂)+ Р (Н ₃)* Р (А / H ₃))=

= (4/15*3/10)/(2/5*1/10+1/3*1/5+4/15*3/10)=3/7. ¨

Дата добавления: 2014-01-15