Последовательное соединение сопротивления, индуктивности и емкости

Основы символического метода расчета цепей синусоидального тока

Расчет цепей переменного синусоидального тока может производиться не только путем построения векторных диаграмм, но и аналитически – путем операций с комплексами, символически изображающими синусоидальные ЭДС, напряжения и токи. Достоинством векторных диаграмм является их наглядность, недостатком – малая точность графических построений. Применение символического метода позволяет производить расчеты цепей с большой степенью точности. Символический метод расчета цепей синусоидального тока основан на законах Кирхгофа и законе Ома в комплексной форме. Уравнения, выражающие законы Кирхгофа в комплексной форме, имеют совершенно такой же вид, как и соответствующие уравнения для цепей постоянного тока. Только токи, ЭДС, напряжения и сопротивления входят в уравнение в виде комплексных величин.

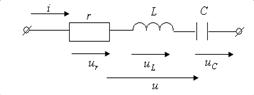Рассмотрим применение метода комплексных ампли­туд в случае последовательного соеди­нения элементов r, L и С (рисунок 6.4).

Рисунок 6.4

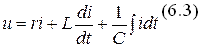Положим, что в уравнении Кирхгофа

заданными являются параметры r, L, С и напряжение 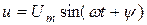, а искомой величиной является ток i. Решение этого дифференциального урав­нения должно дать синусоидальную функцию вида .

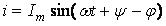Комплексные амплитуды напряжения и тока равны соответственно

Комплекс­ное уравнение, соответствующее уравнению (6.3)

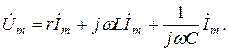(6.4)

Комплексное сопротивление рассматриваемой электрической цепи

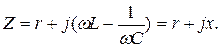(6.5)

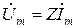
Таким образом, получается уравнение, выражающее закон Ома для комплексных амплитуд и действующих значений.

и 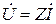. (6.6)

Комплексное сопротивление 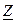в тригонометрической и показательной фор­мах имеет вид

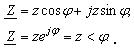(6.8)

Здесь 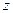- модуль комплексного числа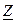,представляет собой полное сопротивление цепи; а 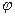— ар­гумент комплексного числа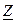

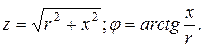(6.9 )

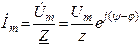На основании (6.6) комплексная амплитуда тока

где 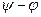- начальная фаза тока. Следовательно, иско­мый ток в тригонометрической форме

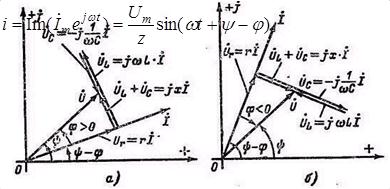Рисунок 6.5

На рисунке 6.5 дана геометрическая интерпретация на комплексной плоскости уравнения (6.4). Рисунок 6.5,а относится к случаю, когда реактивное сопротивление це­пи имеет индуктивный характер (х>0) и 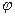>0. Рисунок 6.5,б относится к случаю, когда реактивное сопротивле­ние цепи имеет емкостный характер (х<0), и 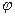<0.

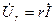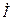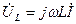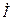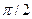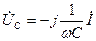Как видно из векторных диаграмм, приведенных на рисунке 6.5, — напряжение на сопротивлении r (сов­падает по фазе с током ), — напряжение на индуктивности L (опережает ток на угол ) и — напряжение на емкости С (отстает от тока I на угол ).

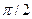Геометрическая сумма векторов 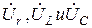дает век­тор приложенного к цепи напряжения U.

Дата добавления: 2014-01-15