
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Общие положения алгебры логики
|
|
|
|
ЛУГАНСК 2009
I-й семестр
Багринцев В.Т.
“КОМПЬЮТЕРНАЯ ЭЛЕКТРОНИКА”
Разработка (или синтез) цифровых устройств, микропроцессорных систем любого уровня, а так же выбор алгоритмов работы этих систем и устройств базируются на знаниях законов алгебры логики (булевой алгебры), которые раскрывают связи между переменными и их функциями, принимающими значения 0 или 1. Символы 0 и 1 в алгебре логики характеризуют состояния переменных и их функций, поэтому их нельзя рассматривать как арифметические числа, т. е. алгебра логики – это алгебра состояний, а не алгебра чисел.
1.1 Операции алгебры логики
Над переменными могут производиться три основных действия: логическое сложение (дизъюнкция), логическое умножение (конъюнкция), логическое отрицание, что соответствует логическим функциям ИЛИ, И, НЕ.
Логическое сложение обозначается символами 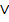 или
или 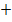 . Логическая функция ИЛИ будет истина (y=1), если хотя бы одна из переменных
. Логическая функция ИЛИ будет истина (y=1), если хотя бы одна из переменных 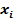 будет иметь значение 1:
будет иметь значение 1:
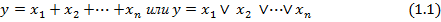
Это выражение можно реализовать электрической схемой, в которой переменные 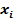 представляются параллельно соединенными замыкающимися или размыкающимися контактами реле или электронными ключами (рис. 1.1), т. е. электрическая схема реализует связь выхода с входом.
представляются параллельно соединенными замыкающимися или размыкающимися контактами реле или электронными ключами (рис. 1.1), т. е. электрическая схема реализует связь выхода с входом.

Рис. 1.1
Информация с входа схемы будет передана на выход, если хотя бы один из контактов замкнут (например, 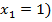 .
.
Таким образом, логическая сумма равна единице, если равна единице одна или несколько переменных:
0 = 0 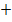 0
0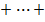 0; 0
0; 0 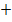 1
1 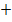 0
0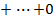 =1; 1
=1; 1 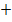 1
1 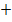 1
1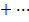
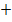 1 =1
1 =1
Логическое умножение (конъюнкция) обозначается точкой или символом  . Логическая функция И будет истина (y=1) в том случае, если все переменные будут иметь значение 1:
. Логическая функция И будет истина (y=1) в том случае, если все переменные будут иметь значение 1:
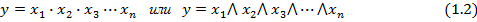
Это выражение реализуется электрической схемой, в которой все переменные 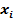 , представляющие собой контакты или электрические ключи, соединены последовательно (рис. 1.2):
, представляющие собой контакты или электрические ключи, соединены последовательно (рис. 1.2):
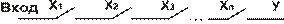
Рис. 1.2
На выходе схемы будет единица 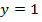 (т. е. информация будет передана с входа на выход) в том случае, если все контакты будут замкнуты:
(т. е. информация будет передана с входа на выход) в том случае, если все контакты будут замкнуты:
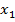 =1,
=1, 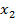 =1, ….
=1, ….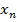 =1;
=1; 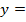 1
1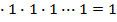
Логическое отрицание (инверсия) обозначается чертой над переменной 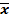 . Электрической схемой, реализующей функцию НЕ, может быть размыкающийся контакт реле или закрытый электронный ключ. При срабатывании реле контакт размыкает электрическую цель, при отключении реле контакт его замыкает электрическую цепь. Таким образом, инверсия единицы равна нулю, инверсия нуля – единице, а двойная инверсия не изменяет значения переменной:
. Электрической схемой, реализующей функцию НЕ, может быть размыкающийся контакт реле или закрытый электронный ключ. При срабатывании реле контакт размыкает электрическую цель, при отключении реле контакт его замыкает электрическую цепь. Таким образом, инверсия единицы равна нулю, инверсия нуля – единице, а двойная инверсия не изменяет значения переменной:
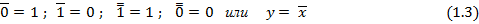
Функция будет равна единице (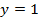 ), если
), если 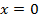 и наоборот.
и наоборот.
Основываясь на эти арифметико - логические действия, можно убедиться в справедливости следующих выражений (аксиом):
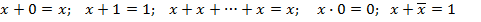
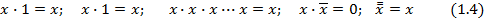
1.2 Основные законы алгебры логики
В алгебре логики существуют четыре основных закона.
1. Переместительный (коммутативный) закон:
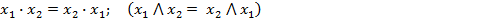

2. Сочетательный или закон ассоциативности:
(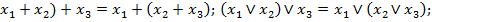
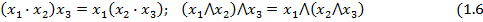
3. Распределительный закон (дистрибутивности):
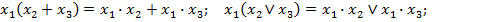
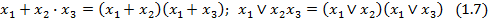
Последнее равенство легко доказывается следующими преобразованиями:
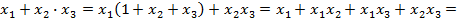
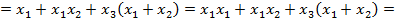
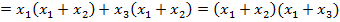
4. Закон отрицания или правило де Моргана:
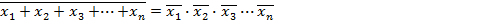

Рассмотрим также два правила, которые часто используются при упрощении логических выражений или синтезе логических устройств.
5. Правило поглощения:

Выражение в скобках – есть одна из аксиом (6.4) алгебры логики. Справедливость аксиомы можно проверить по электрической схеме параллельно соединенных контактов (электронных ключей):

Рис. 1.3
Релейный контакт (электронный ключ) 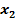 может иметь замкнутое или разомкнутое состояние, а 1 всегда представляется замкнутым контактом, поэтому независимо от состояния ключа
может иметь замкнутое или разомкнутое состояние, а 1 всегда представляется замкнутым контактом, поэтому независимо от состояния ключа 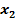 , сигнал всегда будет поступать с входа схемы на выход через замкнутый контакт 1, т. е.
, сигнал всегда будет поступать с входа схемы на выход через замкнутый контакт 1, т. е. 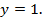
6. Правило склеивания:

Выражение в скобках – это одна из аксиом (1.4) и справедливость его можно проверить по следующей электрической схеме:

Риc. 1.4
При любой комбинации состояний ключей эта цепь будет всегда замкнутой, т. е. y = 1, что и требовалось доказать.
1.3 Основные логические (переключательные) функции
Рассмотренные логические законы и логические правила (аксиомы) широко используются для преобразования, упрощения переключательных функций и различной сложности логических выражений. Всякая логическая функция может быть комбинацией элементарных логических функций И, НЕ, ИЛИ. Если логическая функция содержит все три простейшие функции, то она называется полной или базисом, например,
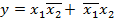
Эта функция может быть реализована двумя логическими элементами НЕ, двумя логическими элементами И и одним элементом ИЛИ.
Функционально полные системы могут состоять, кроме того, и из однотипных несложных логических функций, например, реализующих функцию И-НЕ или ИЛИ-НЕ, которые также могут образовать базис со всеми его свойствами.
Функция И-НЕ или функция Шеффера, означает выражение:

Функция И-НЕ позволяет получить на ее базисе все элементарные логические функции. Например, для получения функции НЕ, достаточно подать на все переменные, кроме одной, константу, равную 1:
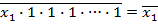
Дл получения функции И можно инвертировать функцию И-НЕ и использовать одну из аксиом (1.4):
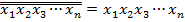
Функция ИЛИ строится в соответствии с правилом де Моргана, для чего отдельно инвертируются переменные, а затем из них строится функция И-НЕ:
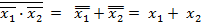
Функция ИЛИ-НЕ или функция Пирса представляется выражением:

Функция ИЛИ-НЕ также позволяет получить все элементарные логические функции НЕ, ИЛИ, И. Выражение (1.12) обращается в функцию
НЕ, если на все переменные, кроме одной, подать константу, равную 0:
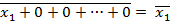
Функция ИЛИ может быть получена путем инвертирования функции ИЛИ-НЕ:
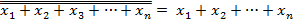
Функция И строится в соответствии с правилом де Моргана, для чего отдельно инвертируются переменные и записывается функция ИЛИ-НЕ:
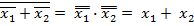
Таким образом, логические функции И-НЕ, ИЛИ-НЕ позволяют получить все элементарные логические функции, а следовательно, создавать логические функции любой сложности.
Рассмотрим также некоторые логические переключательные функции двух переменных, представляющие интерес.
Функция запрета двух переменных по 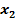

Функция 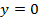 всегда, если
всегда, если 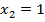 (т.е. запрет по
(т.е. запрет по 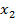 ).
).
Т а б л и ц а 1.1
Таблица истинности.
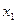
| 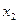
| y |
Из табл. 1.1 видно, что 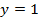 только при
только при 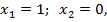 что определяется конъюнкцией переменных.
что определяется конъюнкцией переменных.
Функция запрета двух переменных по 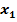
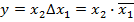
Функция 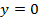 всегда, если
всегда, если 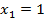 (т.е. запрет по
(т.е. запрет по 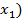
Т а б л и ц а 1.2
Таблица истинности.
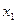
| 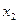
| y |
Из табл. 1.2 следует, что 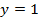 только при
только при 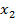 =1 (при условии
=1 (при условии 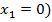 , что определяется конъюнкцией переменных.
, что определяется конъюнкцией переменных.
Функция неравнозначности (функция исключающая ИЛИ)
Функция выполняет операцию суммирования по модулю 2:

Т а б л и ц а 1.3
Таблица истинности
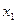
| 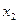
| y |
Из таблицы истинности следует, что функция 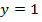 при условии:
при условии:
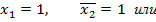
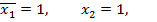
что определяется дизъюнкцией конъюнкций переменных.
Функция равнозначности (функция исключающая 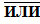 )
)
Функция выполняет операцию инвертирования суммы по модулю 2:

Т а б л и ц а 1.4
Таблица истинности
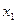
| 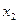
| y |
Из таблицы следует, что функция 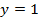 в случаях конъюнкции переменных:
в случаях конъюнкции переменных: 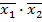 или
или 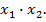
1.4 Упрощение и минимизация логических функций
Разработка цифрового устройства обычно начинается с создания математико-логической модели (т.е. логической функции), в которой по возможности учитываются все необходимые переменные (аргументы) согласно требований, поставленных в техническом задании на создание устройства. Логическая функция при этом может оказаться весьма сложной, поэтому на этом этапе проводится ряд мер по упрощению полученной логической функции.
Процесс упрощения логической функции с целью получения минимальной нормальной формы носит название минимизация. При минимизации уменьшается количество логических элементов, упрощается структурная схема устройства, а следовательно, затраты на его реализацию.
Существует немало методов минимизации логических функций, поэтому в данном разделе рассматриваются самые простые и универсальные:
- метод последовательного исключения переменных;
- метод Квайна (универсальный);
- метод минимизирующих карт Вейча (Карно)
а) Метод последовательного исключения переменных.
Этот метод самый простой, и его реализация сводится к умелому использованию законов и тождеств алгебры логики для упрощения логических функций до вида ДНФ или КНФ.
При наличии в функции сложных элементов, например, инверсий дизъюнкции конъюнкций или конъюнкции дизъюнкций переменных, необходимо освободиться в первую очередь от сложных инверсий, а затем приступить к операциям склеивания элементов и поглощения переменных.
Пример 1. Упростить логическую функцию

Решение:
Логическая функция представлена дизъюнкцией конъюнкций переменных сложных элементов, часть из которых находится под общей инверсией, поэтому в первую очередь освободим эти элементы функции от общих инверсий, используя правила де Моргана:

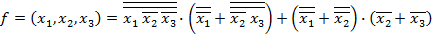
Применив ряд известных аксиом и правил это выражение упрощается:
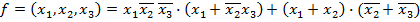
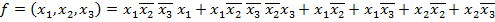
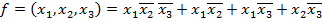
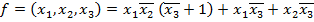
Окончательно логическая функция примет вид ДНФ:
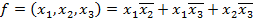
Но эта логическая функция может и не быть минимальной.
2. СИСТЕМЫ СЧИСЛЕНИЯ И АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ
Основными элементами компьютерной электроники являются импульсные и цифровые устройства, вводимая и выводимая информация которых представляется в виде импульсов и цифровых кодовых комбинаций из лог.1 и лог.0.
Выбор системы счисления влияет на характеристики функциональных цифровых устройств: скорость вычислений, объем памяти, сложность алгоритмов вычислений, сложность технической реализации.
С точки зрения реализации оптимальной является двоичная система счисления, строящаяся на двухпозиционных электронных элементах. Числа в такой системе счисления представляются последовательностью цифр 1 и 0, значение (или вес) каждой из которых зависит от ее места или разрядности в числе. Такая система счисления называется позиционной.
Таким образом, система счисления – это алгоритм изображения чисел с помощью символов (цифр), имеющих определенные количественные значения в зависимости от их разрядности.
Каждому разряду присваивается весовой коэффициент в виде основания системы в соответствующей степени. В общем случае представление некоторого числа  в системе счисления с основанием P будет иметь вид степенного полинома:
в системе счисления с основанием P будет иметь вид степенного полинома:
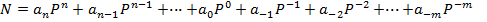
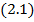 ,
,
где P – основание системы;
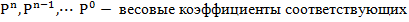
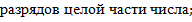
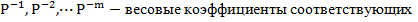
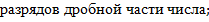
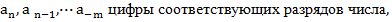
удовлетворяющие неравенству:

Степень полинома определяется как разность количества разрядов k целой части числа минус 1:

2.1 Представление чисел в различных системах счисления
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 651; Нарушение авторских прав?; Мы поможем в написании вашей работы!