Зворотна матриця

Нехай А и В - дві матриці наступного виду:

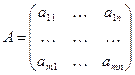і ;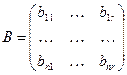

оборотний увага на те, що в першій з них стовпців стільки ж, скільки в другий з них - рядків. У цьому випадку можна побудувати нову матрицю З

,

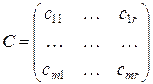називану добутком А на В (пишуть ІЗ=АВ), за правилом

,

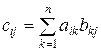де i= 1,...,m і j= 1,...,r. Серед матриць прийнято виділяти й позначати буквою E

наступну матрицю, називану одиничної, -

;

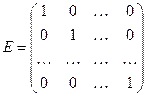пояснимо: одинична матриця завжди квадратна, по її діагоналі коштує 1, а всі інші елементи - нулі, тобто якщо Е=(е_ij), i,j=1,...,n, те

.

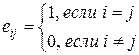Говорять, що квадратна матриця А и квадратна матриця В того ж розміру є зворотними по відношенню друг до друга, якщо виконано хоч одне з матричних рівностей - або АВ=Е або ВА=Е. Можна перевірити, що якщо одне із цих матричних рівностей виконується, то виконується й інше. Про всякий випадок пояснимо, що слова «матрична рівність» означають рівність заелементне, тобто якщо має місце рівність матриць U=V, те це означає, що в них рівні кількості рядків і рівні кількості стовпців і при цьому u_ij=v_ij для всіх i і j. Зокрема, система лінійних алгебраїчних рівнянь із п.3 Лекції 1 може бути записана у вигляді AX=B, де

,

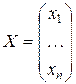а А и В мають той же змив, що й у п.3 Лекції 1.

Неважко помітити, що якщо для квадратної матриці А потрібно знайти зворотну матрицю В, те треба вирішити n систем лінійних алгебраїчних рівнянь із однієї й тої ж матрицею: запишемо матричну рівність АВ=Е поелементно (тут усього вийде n² рівностей), причому будемо послідовно дорівнювати стовпці - перший стовпець лівої частини до першого стовпця правої частини, другий стовпець лівої частини до другого стовпця правої частини й т.д. –

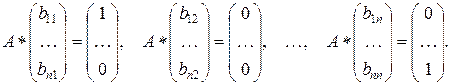
Із цього спостереження треба, що знайти зворотну матрицю можна вирішуючи одночасно n систем лінійних алгебраїчних рівнянь із однієї й тією же матрицею А.

Дата добавления: 2014-01-15