КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 11. 11.1. Задача апроксимації функції
|
|
|
|
ЗАДАЧА АПРОКСИМАЦІЇ ФУНКЦІЇ. ІНТЕРПОЛЯЦІЙНИЙ БАГАТОЧЛЕН ЛАГРАНЖА Й РІЗНІ ФОРМИ ЙОГО ЗАПИСУ. ЗАДАЧА РІВНОМІРНОГО НАБЛИЖЕННЯ ФУНКЦІЇ. МЕТОД НАЙМЕНШИХ КВАДРАТІВ. БАГАТОЧЛЕНИ БЕРНШТЕЙНА
11.1. Задача апроксимації функції.
Нехай на відрізку [ a,b ] деяка функція f(x) задана лише в деяких точках 
, тобто відомі її значення
, які, як правило, збирають у таблицю:
| x | x0 | x1 | ... | xn |
| f(x) | y0 | y1 | ... | yn |
Крім того, нехай задана деяка точка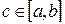 
. Задача апроксимації функції 
полягає в тому, щоб по наявній таблиці знайти число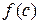 
з відомим ступенем точності. Слово «апроксимація» означає «наближення».
Легко зрозуміти, що якщо на функцію не накладаються ніякі додаткові умови, то постановка задачі безперспективна. Ми будемо далі припускати, що функція має всі похідні. Виявляється, що в цьому випадку по наявним n+1 значенням можна знайти ще одне й оцінити, наскільки воно точно.
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 297; Нарушение авторских прав?; Мы поможем в написании вашей работы!