Багаточлени Бернштейна

Припустимо, що функція задана у відрізку [0,1] у точках 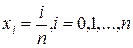, при деякому фіксованому n. У цьому випадку можна побудувати багаточлен Бернштейна

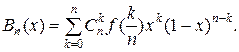
Можна довести, що при 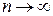багаточлени 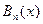прагнуть до функції рівномірно по x; крім того, для будь-якого конкретного цілого має місце граничне співвідношення для похідних:

Нарешті, відомо, що якщо число 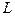задовольняє нерівності на всьому відрізку [0,1], те для кожного 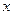із цього відрізка виконується нерівність:

.

Це, звичайно, дозволяє оцінювати помилку, що виникає при відповідній інтерполяційній заміні.

Сказане вище для випадку функції один змінної можна узагальнити на випадок двох і більше змінних. Ми обмежимося узагальненням тільки на випадок двох змінних.

Отже, нехай є функція на квадраті

,

причому реально вона задана у вузлах решітки

,

при заздалегідь фіксованих натуральних числах і . Побудуємо по цій інформації наступний багаточлен від двох змінних:

,

де - біноміальні коефіцієнти. Це - багаточлен Бернштейна для заданої функції на заданих решітці. З його допомогою так само можна здійснювати інтерполяцію, приймаючи його значення в тій або іншій точці квадрата за значення самої функції. Можна довести, що для будь-якої точки квадрата має місце нерівність:

,

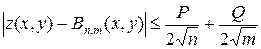яке й дозволяє оцінити погрішність інтерполяції. Тут константи й задовольняють у розглянутому квадраті нерівностям

.

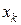Зауваження. Випадок один змінної розглядався вище на відрізку [0,1], а випадок двох змінних - в одиничному квадраті. У дійсності, розгляди можливі на будь-якому відрізку [ a,b ] і на будь-якому прямокутнику [ a,b;c,d ]. Для цього у вихідній ситуації (тобто на довільному відрізку або на довільному прямокутнику) потрібно зробити лінійну заміну змінних. Докладніше: нехай функція задана в точках відрізка , де при деякому фіксованому

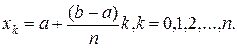
Покладемо

тоді

якщо тепер у покласти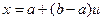, то виникне ситуація функції , заданої вже на відрізку [0,1]. Аналогічно, у випадку двох змінних треба зробити заміну

,

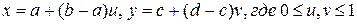після чого виникне ситуація одиничного квадрата.

Дата добавления: 2014-01-15