Канонічна форма основного завдання опуклого програмування

Нехай є яке-небудь основне завдання опуклого програмування: потрібно

знайти мінімум функції

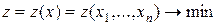
при обмеженнях:

,

причому всі зазначені тут функції - - опуклі. Уведемо нову змінну 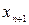й сформулюємо наступне завдання:

знайти мінімум функції

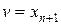
при обмеженнях:

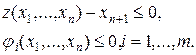
Помітимо, що це - теж завдання опуклого програмування. Припустимо, що її вдалося вирішити й виявилося, що відповідна екстремальна точка є ; можна довести, що в цьому випадку екстремальною крапкою у вихідному завданні опуклого програмування виявляється точка 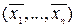. Тому прийнято розглядати завдання опуклого програмування в наступній канонічній формі: знайти мінімум лінійної функції

при обмеженнях:

причому всі функції в обмеженнях - опуклі.

Надалі ми припускаємо в цій темі, що всі обговорювані функції - гладкі (тобто мають безперервні похідні всіх порядків). Крім того, нагадуємо, що мовчазно передбачається, що існує внутрішня точка, що задовольняє всім обмеженням.

14.4. Пошук вихідного наближення.

Як відзначалося в п.2, пошук рішення основного завдання опуклого програмування являє собою побудова послідовності точок 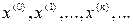в n- мірному просторі, що сходиться до точки екстремальної (шуканої). Пояснимо це. Якщо 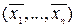- шукана екстремальна точка й

,

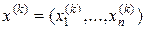де послідовність 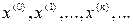прагне до точки »

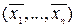означають, що числова послідовність

прагне до нуля.

Початок згаданої послідовності точок - точка 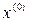- називається початковим наближенням. Ми опишемо зараз спосіб знайти .

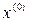Нехай спочатку m= 1. Щоб знайти точку a таку, що , можна діяти, наприклад, так: шукати мінімум функції багатьох змінних. Або інший спосіб: покласти всі координати, крім однієї, рівними конкретним числам, а що залишилася підібрати, відповідно до вимоги.

Припустимо, що для m=k відшукання крапки a такий, що 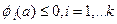вже відбулося. Тоді пошук точки a, для якої буде виконана ще одна умова - - можна розглядати як пошук точки мінімуму опуклої функції 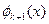при обмеженнях 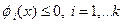. Знайдена екстремальна точка буде, звичайно, задовольняти всім необхідним нерівностям (нагадаємо, що споконвічно передбачається випадок наявності внутрішньої точки!)

Процедура пошуку мінімуму в завданні опуклого програмування буде описана в наступній лекції. Як уже згадувалося, вона виходить тільки з початкового наближення 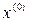. Тому описаний тут спосіб побудови цього початкового наближення фактично звівся до двох процедур:

Процедура 1. Знайти точку, що задовольняє єдиній нерівності 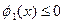. Нехай це буде крапка .

Процедура 2. Знайти екстремальну точку в кожному з наступних завдань опуклого програмування:

Завдання 1. Цільова функція 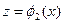, умови: 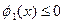. Початкове наближення - точка . Нехай результатом буде точка .

Завдання 2. Цільова функція 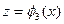, умови . Початкове наближення - точка . Нехай результатом буде точка .

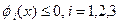Завдання 3. Цільова функція , умови .. Початкове наближення - точка . Нехай результатом буде точка .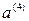

І так далі, аж до відшукання початкового наближення .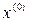

Принципове зауваження. Якщо на одному з описаних етапів мінімум цільової функції виявиться позитивним, те, як легко помітити, процедура переривається, тому що позитивність мінімуму означає відсутність шуканої точки.

Дата добавления: 2014-01-15