Поле направлений

У любого дифференциального уравнения обычно бывает бесконечно много решений. Чтобы это наглядно продемонстрировать, рассмотрим график произвольного решения 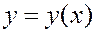на плоскости .

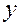
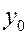
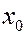
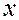
Пусть 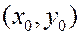произвольная точка графика. Найдем уравнение касательной к графику в данной точке. В общем виде уравнение касательной к кривой 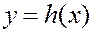может быть записано так

.

В нашем случае , следовательно, уравнение касательной имеет вид

.

Направляющий вектор касательной равен .

Важный факт: касательной вектор к решению дифференциального уравнения в точке 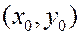мы можем найти, даже не зная самого решения!

Определение. Векторное поле (то есть множество векторов на плоскости, “прикрепленных” к каждой точке этой плоскости) называется полем направлений дифференциального уравнения.

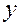
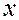
Решение дифференциального уравнения по отношению к полю направлений является огибающей. Легко понять, что таких огибающих бесконечно много, однако для дифференциальных уравнений с гладкой правой частью через каждую точку плоскости проходит единственная огибающая.

Задачей Коши для уравнения называется краевая задача вида .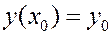

Теорема о существовании и единственности решения задачи Коши утверждает, что, если функция и её частная производная непрерывны по совокупности аргументов, то найдется такой интервал 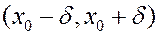, на котором имеется, и притом единственное, решение уравнения , для которого .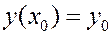

Определение. Общее решение дифференциального уравнения 1-го порядка есть соотношение вида 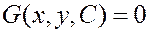такое, что

1) для любого решения уравнения найдется константа , для которой ;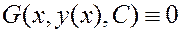

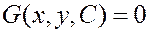2) для любой константы неявное уравнение определяет некоторое решение дифференциального уравнения .

Имеется несколько стандартных уравнений первого порядка, в которых нахождение общего решения сводится к взятию подходящих интегралов.

Уравнения с разделяющимися переменными.

Эти уравнения имеют вид .

Решение уравнения сводится к преобразованию

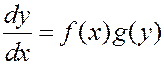Û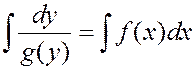

Теорема. Общее решение дифференциального уравнения может быть записано в виде .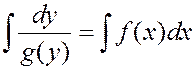

Пример. Найти общее решение дифференциального уравнения

Решение. Запишем 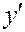как 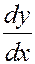и перегруппируем правую и левую части уравнения, так чтобы слева от знака равенства остались члены, зависящие только от 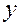, а справа – только от .

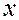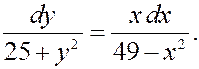
Вычисляя интеграл от левой части, получим:

.

Для правой части получаем

.

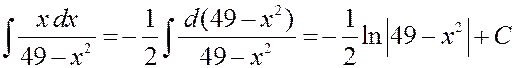Окончательно, .

Дата добавления: 2014-01-15