
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Кроме того, если выполнено условие
|
|
|
|
4) А В Ì W,
то имеем поле событий.
Очевидно обобщение на любое конечное число событий 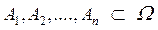 .
.
Событие, которое никогда не происходит (то есть не содержит ни одной точки), называется невозможным, обозначается символом Æ и
" (A Ì W) Þ (Æ Ì A).
Событие А = W всегда происходит и называется достоверным, при этом полагаем ` W = Æ.
События А 1, А 2 Ì W несовместны, если А 1 Ç А 2 = Æ (то есть события А 1 и А 2 не имеют общих точек).
События А 1, А 2,..., Аn образуют полную группу, если W Í 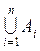 , а если Аi, i = 1, 2, …, n, попарно несовместные, то есть " i ¹ j, j = 1, 2, …, n, Аi Ç Аj = Æ, тогда
, а если Аi, i = 1, 2, …, n, попарно несовместные, то есть " i ¹ j, j = 1, 2, …, n, Аi Ç Аj = Æ, тогда 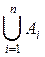 = W.
= W.
Если каждое появление события А влечет за собой появление события В, то говорят, что А есть часть В, то есть А Ì В.
Многие задачи теории вероятностей содержат бесконечное число исходов (например, точки на отрезке прямой, поверхности и др.), и мы можем столкнуться с трудностями теоретического характера, если любое подмножество отрезка или поверхности будем считать событием. Чтобы их избежать, мы вводим специальный класс ℱ подмножеств, состоящий из несчетных множеств, где любое его подмножество есть событие. Формально это выглядит следующим образом.
Пусть пространство W - произвольное множество (в том числе, несчетное), а ℱ класс подмножеств из множества W.
ℱ называется s- алгеброй, если
1) W Ì ℱ,
2) " Аi Ì ℱ, i Î N Þ 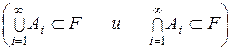 ,
,
3) А Ì ℱ Þ 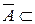 ℱ.
ℱ.
Таким образом, алгебра событий замкнута относительно конечного числа теоретико-множественных операций (объединения, пересечения, отрицания), а s- алгебра замкнута относительно бесконечного числа этих операций.
Замечание. По условию, класс подмножеств ℱ содержится в пространстве W и одновременно, сам содержит это пространство. Возможность такой формализации становится понятной, если считать ℱ оператором «наведения порядка» в W. Тогда, если, например, W интерпретировать как единичный объем жидкости, а ℱ - как губку, то, если вся жидкость находится в губке всюду плотно, получается, что с одной стороны, губка находится в жидкости, а с другой стороны, вся жидкость находится в губке.
Мерой или количественной оценкой случайных событий из W служит вероятность р – число, удовлетворяющее следующим аксиомам.
Аксиома 1. Любому событию А Ì W, удовлетворяющему условиям 1) – 3), поставлено в соответствие неотрицательное число p = Р { А }, называемое его вероятностью.
Аксиома 2. Р { W } = 1.
Аксиома 3. Если события А 1, А 2,..., Аn,... попарно несовместны, то
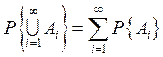 .
.
Пространство W, с заданной на нем алгеброй (s - алгеброй) событий и определенной для каждого события вероятностью, которая удовлетворяет аксиомам 1-3, является центральным понятием, определяющим аксиоматический подход к построению теории вероятностей, введенный А.Н. Колмогоровым в 30-х годах прошлого века [2].
Определение. Тройку (W,ℱ, Р) будем называть вероятностным пространством.
Замечание. В данном курсе теории вероятностей мы обсуждаем только такие случаи, для которых любое подмножество W есть событие, а потому введение s- алгебры ℱ излишне. Однако в целях конструктивности изложения мы будем писать (W,ℱ, Р), подразумевая под вероятностным пространством (W, Р).
|
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 379; Нарушение авторских прав?; Мы поможем в написании вашей работы!