Интегральная теорема Муавра-Лапласа

Теорема. Пусть в n независимых испытаниях вероятность появления события А в каждом испытании постоянна и равна р, 0< р < 1, тогда, для любых -¥ < а < b < ¥, равномерно относительно а, b, при n ® ¥, имеет место асимптотическая оценка

, (16)

где j(х) - кривая Гаусса, , .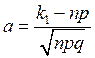

Функция называется функцией Лапласа.

Так как Р_n {0 £ k £ n } = 1 для любого n, то из (16) должно следовать, что .

В самом деле, положим ℑ , тогда

ℑ ².

Введем полярные координаты:

, , , , .

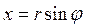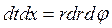Отсюда

ℑ ² = , ℑ = 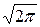- интеграл Пуассона.

Следовательно, ._▼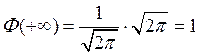

Для практических приложений вместо (16) используют формулу:

Р { k₁ £ k £ k₂ }» Ф (в) – Ф (а), (17)

где

, .

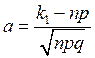Учитывая, что Ф (+¥) = 1, легко получить Ф (х) + Ф (- х) = 1.

В самом деле, пусть х > 0, тогда , а .

Отсюда

Ф (х) + Ф (- х) =

Функция - табулирована, ее значения приведены в табл. 4 приложения.

Таблица составлена для х < 0, а для х > 0, значения находятся по формуле

Ф (х) + Ф (- х) = 1.

Пример. Решить пример п 1.5, б).

Решение. Имеем

, , .

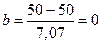По табл. 5 приложения находим

.

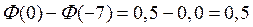Отсюда .

Сравнивая решение задачи п.1.5. а), б), можно предположить, что, так как – наивероятнейшее число, с большой вероятностью реализуется событие { 40 £ k £ 60}, с центром в точке k ₀:

.

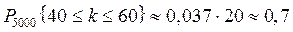Заметим, что 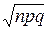характеризует средние отклонения от среднего значения np (чем меньше 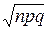, тем «круче» кривая Гаусса в точке симметрии).

Дата добавления: 2014-01-15