Свойства функции распределения. Пусть дано произвольное вероятностное пространство (W,ℱ,Р)

Часть 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ФУНКЦИИ РАСПРЕДЕЛЕНИЯ

Пусть дано произвольное вероятностное пространство (W,ℱ, Р).

Введем одно из основных понятий теории вероятностей – случайную величину. Интуитивно, случайная величина – это переменная (функция), которая в результате эксперимента принимает одно из множества своих возможных значений.

Определение: Измеримая [2] функция x, определенная на пространстве элементарных событий W и принимающая значения из области действительных

чисел, называется случайной величиной

x = x (w), w Î W, x Î R. (21)

Поскольку для любого элементарного события w Î W определена вероятность его реализации, то очевидно, что каждое значение случайной величины так же имеет свою вероятность. Таким образом, с каждой случайной величиной связано распределение вероятностей (в определении это измеримость).

Различают два основных вида случайных величин: дискретные и непрерывные.

Случайная величина, которая принимает конечное или счетное число значений, называется дискретной.

Например, к дискретным случайным величинам относятся:

а) число отказов технического устройства за определенное время;

б) количество посетителей столовой в каждый рабочий день за месяц;

в) число появлений гербов при подбрасывании монеты в серии из n испытаний.

Случайная величина называется непрерывной, если она принимает значения из интервала или, может быть, всей действительной оси.

Например, к непрерывным случайным величинам относятся:

а) время работы технического устройства до первого отказа;

б) отсутствие посетителей в столовой в течение не более чем один час;

в) величина ошибки измерения физических величин.

Дискретная случайная величина полностью определяется своим законом распределения, который можно представить в виде табл. 1:

Таблица 1

x	x 1	x 2	…	xn	…
p	p 1	p 2	…	pn	…	(S pi =1)

где х_i, i Î N возможные значения случайной величины, а р_i – соответствующие им вероятности. При этом сумма вероятностей всех значений случайной величины всегда равна единице.

В общем случае, случайная величина полностью определяется своей функцией распределения.

Определение. Функцией распределения F (х) случайной величины x называется вероятность события { x < х }, х Î R, то есть

F (х) = Р { x < х }, х Î R. (22)

Функция распределения существует для любой случайной величины.

1) Монотонность: "(х ₁ £ х ₂) Þ (F (х ₁) £ F (х ₂);

2) непрерывность слева:

;

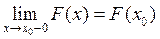3) число разрывов 1-го рода не более чем счетно (ступенчатая функция);

4) F (-¥) = 0;

5) F (+¥) = 1.

Любая функция, удовлетворяющая свойствам 1) – 5), является функцией распределения и обратно.

Для любой дискретной случайной величины можно построить ее функцию распределения. Более того, можно сказать, что величина x = x (w) называется случайной, если она имеет функцию распределения.

Определение. Индикатором события А называется случайная величина:

I_А (w) =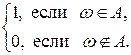

Пример 1. Построить функцию распределения индикатора события А, если известно, что Р { w Î A }= р.

Решение. Случайная величина I_А (w) – дискретная. Закон ее распределения имеет вид:

IА			.
р	1- р	р

Функцию распределения определим формулой:

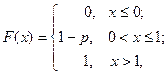
график которой представлен на рис. 6.

Рис. 6

Очевидно, что вероятностная характеристика случайной величины, полученная из функции распределения с помощью формальных математических операций и определенная на всей действительной оси, несет столько же информации о случайной величине, что и сама функция распределения. Исключение могут составлять некоторые точки действительной оси, число которых не более чем счетно.

К такой характеристике можно отнести плотность.

Определение. Функция r (х), удовлетворяющая условиям:

а) r (х) ³ 0, " х Î R,

б) ,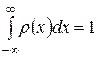

называется плотностью случайной величины x.

Из определения видно, что плотность играет ту же роль, что и закон распределения дискретной случайной величины.

Физически, плотность характеризует распределение единичной массы на действительной оси. Ёе изменение на участке длиной D х, примыкающего к точке х, оценивается интегралом

.

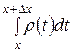Дата добавления: 2014-01-15