Многомерные случайные величины

Развитие аппарата многомерных случайных величин в теории вероятностей так же важно, как и развитие функций нескольких переменных в математическом анализе.

Пусть имеем вероятностное пространство (W, ℱ, Р), (W совпадает с Rⁿ) с заданными на нем случайными величинами x ₁= x ₁(w), x ₂= x ₂(w),…, x_n = x_n (w), w Î W.

Определение. Случайную величину ` x (w) = (x ₁, x ₂, …, x_n) назовем n – мерным случайным вектором, являющимся отображением W ® Rⁿ. Отображение измеримо, в том смысле, что для любого множества из класса ℱ определена функция распределения.

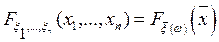, где 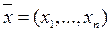. (45)

Функция распределения (45) однозначно определяет распределение вероятностей Р { x ₁< х ₁, x ₂< х ₂,…, x_n < x_n } и обладает свойствами, вполне аналогичными свойствам функции распределения одной переменной, а именно, :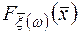

1) неубывающая по каждому аргументу вектора ;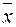

2) ;

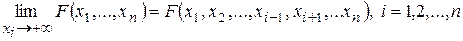3) непрерывна слева по каждому аргументу;

4) ;

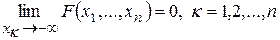5)

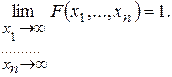
Дальнейшее построение теории многомерных случайных величин приведем для двухмерного случайного вектора (x, h).

Пусть W не обязательно совпадает с R ². Рассмотрим случайный вектор (x, h) Î W_x,h Ì R ², где W_x,h = W_x ´ W_h. Любое подмножество А Ì W_x,h назовем событием. Класс ℱ определим как алгебру событий, каждое из которых можно получить из множеств

((x < х)&(h < у)), где х Î W_x, у Î W_h.

Вероятность события А определим как

Р_x,h { A }= Р { w /(x (w) & h (w))Î A }," А Ì W _x,h.

Тем самым построено вероятностное пространство (W _x,h, Р_x,h), как частный случай рассмотренного ранее.

Из свойств функции распределения легко получить:

а) Р { а ₁ £ x < в ₁, h < у } = F (в ₁, у) - F (а ₁, у)

Графическая иллюстрация представлена на рис. 17 (включение границы в допустимую область обозначено жирной чертой).

б) Р { а ₁ £ x < в ₁, а ₂ £ h < в ₂} = F (в ₁, в ₂) - F (а ₁, в ₂) - F (в ₁, а ₂) + F (а ₁, а ₂)

Графическая иллюстрация представлена на рис. 18.

Рис. 17 Рис. 18

Распределение вероятностей случайного вектора назовем дискретным, если он принимает не более, чем счетное число значений.

Распределение случайного вектора назовем абсолютно непрерывным, если для любого подмножества А, со значениями из R ²,

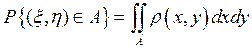
или в эквивалентной форме

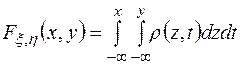. (46)

Функция r (х, у) называется плотностью распределения случайного вектора (x, h). Из (46) следует, что

.

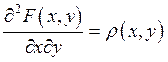Если существует плотность r(х, у), то существуют и плотности r_x (х), r_h (у).

Рассмотрим два примера, часто используемые в приложениях.

Пример (полиномиальное распределение).

Пусть (x, h) - целочисленный случайный вектор. Распределение (x, h) зададим формулой:

,

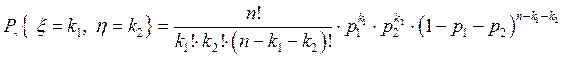где 0 £ к ₁ + к ₂ £ n, р ₁ = Р { А ₁}, р ₂ = Р { А ₂}, 1 - р ₁- р ₂ = Р { W (А ₁È А ₂)}, А ₁, А ₂ Ì W, А ₁ Ç А ₂ = Æ.

Применим описанное распределение при построении математической модели процесса разделения сыпучих материалов [7].

При разделении сыпучего материала на три группы по среднему диаметру частиц (события А_i) установлено, что вероятность Р { А_i } частицы принадлежать группе i равна р_i, i =1,2,3. Распределение вероятностей, того, что среди n частиц к_i частиц принадлежит группе i (к ₁+ к ₂+ к ₃= n) определяется по формуле полиномиального распределения, где к ₃ = n - к ₁ – к ₂.

Пример (Двумерное нормальное распределение).

Пусть дана двумерная случайная величина (x, h). Будем говорить, что она нормально распределена, если ее функция распределения имеет вид:

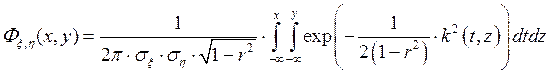
где 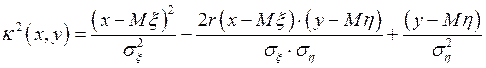- называется эллипсом рассеивания [3], а 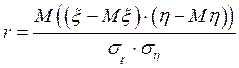- называется коэффициентом корреляции, о котором будем говорить ниже.

Дата добавления: 2014-01-15