Моменты многомерных случайных величин

Определим, по аналогии, начальные и центральные моменты системы двух случайных величин в предположении существования их ряда распределения (или плотности).

Определение. Начальным моментом порядка (к + r) системы случайных величин (x, h) называется число

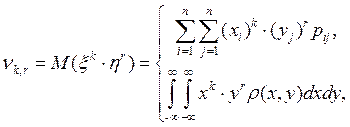
	если (x, h) - дискретная
если (x, h) - непрерывная

В частности, n _1,0 = Mx, n _0,1 = Mh, n Î N.

Определение. Центральным моментом порядка (к + r) системы случайных величин (x, h) называется число

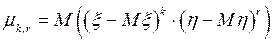, (57)

в частности , .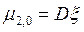

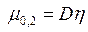Выясним что представляют собой начальный момент n _1,1 и центральный момент m _1,1 системы (x, h).

Рассмотрим более общую задачу. Пусть x₁, x₂, …, x_n - произвольные случайные величины. Вычислим дисперсию их суммы:

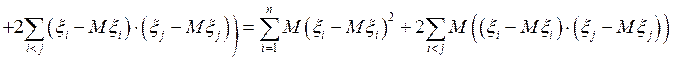или

. (58)

Число слагаемых во второй сумме, правой части (58), равно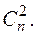

Если бы случайные величины были независимы, то, в силу свойств математического ожидания,

, .

Число 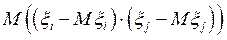, в формуле (58), является вторым смешанным центральным моментом m_1,1 пары случайных величин x_i, x_j.

Его можно рассматривать как меру зависимости случайных величин.

Определение. Ковариацией случайных величин x, h называется математическое ожидание произведения их отклонений

. (59)

Ковариация существует, если существуют дисперсии каждой из случайных величин. Очевидно, что дисперсия есть частный случай ковариации, так как при x = h имеем .

Если случайные величины независимы, то ковариация равна 0. Утверждение сразу следует из свойств математического ожидания отклонений этих величин. Обратное неверно.

Вместо формулы (59) часто используется формула

. (60)

В самом деле, имеем

. _▼

Пример. (Игра в лотерею). У каждого играющего в лотерею свой номер. Карточки с номерами собирают и тщательно тусуют. Затем по очереди, в соответствие с номером, игроки подходят и берут карточки. Получает приз тот, кто взял свой номер. Оценить, сколько призов в среднем следует приготовить.

Решение. Определим сл. в. x_к =

А_к ~{игрок с номером к вытащил карточку с номером к }. Пусть 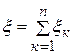- случайная величина, характеризующая число призеров. Ясно, что свою карточку игрок берет с вероятностью n ^-1:

, , ,

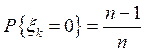но тогда

,

то есть, имеем одно совпадение при любом n.

Найдем дисперсию:

, ,

,

.

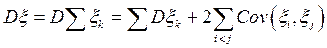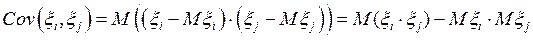Из определения следует, что может быть равно 1 или 0, причем , если обе карты на своем месте, то есть , .

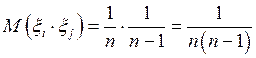Итак, , а так как число слагаемых у второй суммы есть 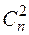, то

.

Таким образом, с учетом средних отклонений, получается, что независимо от числа игроков следует приготовить приза в среднем.

Пример. Пусть случайная величина распределена равномерно в круге D радиуса R (для простоты центр круга поместим в начало координат). Определим плотность

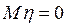Вычислим В силу симметрии, , . Далее,

,

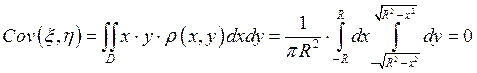то есть x, h некоррелированы, хотя и зависимы. В самом деле, имеем

, ,

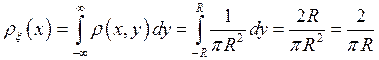тогда

.

Задача. Доказать, что для нормального распределения случайных величин x, h из некоррелированности вытекает их независимость.

Из примера видно, что величина ковариации зависит от размерности случайных величин x, h. Целесообразно ввести безразмерную характеристику, которая будет являться мерой зависимости случайных величин.

Определение. Случайная величина x * называется нормированной, если Мx *=0, Dx *= 1. Любую случайную величину x можно нормировать заменой

.

Определение. Коэффициентом корреляции r (x, h) случайных величин x, h, входящих в двумерную случайную величину (x, h), назовем нормированную ковариацию:

.

Если r (x, h) = 0, то говорят, что случайные величины x, h некоррелированы. Независимые случайные величины всегда некоррелированы.

Если рассматривать геометрический образ случайных величин в декартовых координатах, то для их некоррелированности достаточно, чтобы их совместное распределение было симметрично относительно прямой параллельной любой из осей координат.

Дата добавления: 2014-01-15