Свойства коэффициента корреляции

1) .

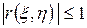В самом деле, имеем

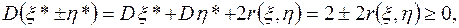
или

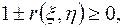что эквивалентно неравенству . _▼

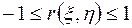2) если x и h независимы, то . Доказательство следует из независимости x * и h *._▼

3) тогда и только тогда, когда случайные величины линейно зависимы, то есть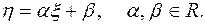

Если a < 0, то r (x, h) = -1, если a > 0, то r (x, h) = 1.

Пусть h = ax + b, тогда

._▼

Обратно, пусть . Возьмем r (x, h) = -1,

тогда

, следовательно .

Возвращаясь к x, h, получаем

.

Для r (x, h) = 1, возьмем _▼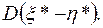

4) Если r (x, h) ¹ 0, то случайные величины зависимы.

Из свойств коэффициента корреляции следует, что он характеризует тесноту линейной связи в том смысле, что с возрастанием одной случайной величины другая линейно увеличивается (если r (x, h)>0) или линейно уменьшается (если r (x, h) < 0), в среднем.

Пусть имеем набор случайных величин x₁, x₂, …, x_n, представляющих некоторый объект для исследования. Математический анализ этого объекта можно проводить, если известны:

а) математические ожидания Мx_i,

б) дисперсии случайных величин Dx_i,

в) парные коэффициенты корреляции r_ij, число которых равно 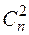, где i, j = 1, 2, …, n.

Для оценки совокупного поведения системы случайных величин, часто рассматривают корреляционную матрицу

,

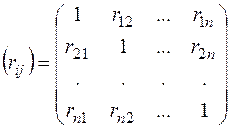где r_ij = r_ji – коэффициенты корреляции случайных величин x_i, x_j.

Изучение этой матрицы задача достаточно сложная и выходит за рамки данного курса [1].

Замечание. Можно рассматривать корреляционную матрицу, элементами которой являются корреляции случайных величин, а по главной диагонали идут их дисперсии. По такой матрице можно судить о величине рассеяния системы случайных величин относительно их среднего значения.

Еще одним видом зависимости случайных величин являются линии регрессии.

Пусть имеем пару (x, h) = (x (х), h (y)).

Определение. Условным математическим ожиданием случайной величины h (или x), при фиксированном значении случайной величины x = х, (или h = у) назовем число

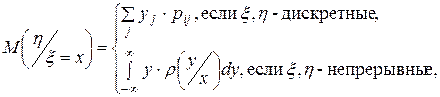(61)

(62)

Из формул (61), (62) видно, что при изменении значений х (значений у) изменяется и величина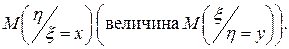

Определение. Функция 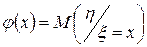называется функцией регрессии случайной величины x на h. Аналогично, 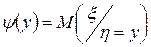- функция регрессии случайной величины h на x.

Кривые, которые заданы функциями и 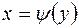, называются линиями регрессии. Ясно, что функции j, y не являются, вообще говоря, обратными, поскольку взаимное влияние случайных величин друг на друга, как правило, различно. Это становится очевидным, если заметить, что при фиксированном значении x = х, значение у = j (х) определяется как условное среднее значений у Î У, которое может даже и не принадлежать множеству У.

Разумно считать, что линии регрессии у = j (х) и 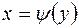различны и имеют, как правило, сложную функциональную зависимость.

Нахождение истинной линии регрессии задача трудновыполнимая. На практике, как правило, поступают следующим образом.

Если, из каких-либо соображений, общий вид линии регрессии известен, например, у = j (a, b, g), то задача состоит в нахождении числовых параметров a, b, g, которые обычно являются композицией из моментов случайных величин. Эта задача решаемая.

Другим, наиболее часто используемым в инженерных расчетах подходом, является приближение линии регрессии многочленом степени n. Приближение тем точнее, чем выше его степень. Обычно выбирают метод наименьших квадратов (М.Н.К.) [4]. Пусть задан класс многочленов, накладывающий на выборку одинаковое число связей, которое равно числу неопределенных коэффициентов многочлена. Наилучшее уравнение приближенной регрессии дает тот многочлен степени n, для которого наименьшее значение имеет функция 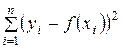, где (х_i, y_i) –совокупность опытных данных.

Пример. Пусть линия регрессии приближается линейной функцией, то есть

.

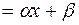Здесь означает, что истинная линия регрессии у = j (х) заменяется на линейную функцию.

Требуется подобрать коэффициенты a, b так, чтобы эта линейная функция была наилучшей.

Решение. Рассмотрим коэффициент корреляции, имеем

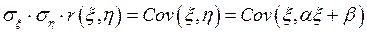
где , а , .

Учитывая (60),

,

или

.

Отсюда

.

Для нахождения b заметим, что, если линия регрессии линейна, то 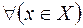справедливо , то есть

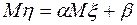
или

.

Таким образом,

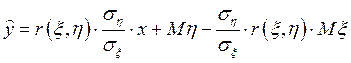. (63)

Аналогично получаем

. (64)

Упражнение. Показать, что те же самые результаты дает метод наименьших квадратов.

Если , то случайные величины зависимы и оцениваются острым углом между прямыми (63) и (64).

а) б)

Рис. 25

На рис. 25 а), коэффициент корреляции r (x, h) > 0, так как с увеличением значений x, значения h увеличиваются. На рис. 25 б), коэффициент корреляции r (x, h)< 0, так как с увеличением значений x, значения h убывают. Если прямые перпендикулярны, то r (x, h) = 0. Это означает, что случайные величины некоррелированы.

Дата добавления: 2014-01-15