Случайные процессы

Пусть имеем произвольное вероятностное пространство (W,ℱ, R), на котором задана случайная величина x = x (w), w Î W. Рассмотрим функцию j (t)= x (w, t), где t Î T, Т – множество, интерпретируемое нами как время.

Определение. Семейство случайных величин x (t) параметра t Î Т, определенное для каждого w ÎW, называется случайным процессом.

На вероятностном пространстве можно задать любое конечное, или даже бесконечное, семейство случайных величин. Однако, если они независимы, то такой процесс трудно назвать случайным. Отличительной особенностью случайного процесса является, именно, зависимость случайных величин, которая осуществляется через связующий параметр t. Задание вида зависимости приводит к возникновению классов случайных процессов (например, процессы с независимыми приращениями [2], марковские процессы [5], пуассоновские процессы [8] и др.), каждый из которых имеет свою, наиболее эффективную область применения. Способы описания случайных процессов, в основном, индивидуальны и приспособлены под тот или иной класс. Существует развитая общая теория случайных процессов [6], которая является в свою очередь, частью общей теории случайных функций.

Пример 1. Последовательность случайных величин x₁, x₂, …, x_n, …, являющаяся результатом работы датчика случайных чисел, образующего двухзначные целые числа в моменты времени t Î{1,2,…}, образует случайный процесс. В этом случае говорят о случайном процессе с дискретным временем и дискретными состояниями.

Пример 2. Срок службы фильтра, модулей по очистке воды, можно рассматривать как случайный процесс со временем t Î Т =[0, Т ₁], где пространство элементарных событий W = {хлор, нефтепродукты, фенол, пестициды, тяжелые металлы и др.}, Т ₁ – срок службы фильтра. Здесь случайный процесс с непрерывным временем и дискретным числом состояний.

Пример 3. Пусть время работы технического устройства является случайной величиной x с экспоненциальной функцией распределения

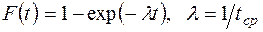, (63)

t_ср – среднее время наработки прибора на отказ.

Число отказов к = 0,1,2,… n прибора за время Т образует случайный процесс с непрерывным временем и дискретными состояниями.

Пусть имеем случайный процесс x (t) = j (w, t). При любом допустимом значении t = t ₁ случайный процесс становится случайной величиной x (t ₁)= j (w, t ₁), для которой имеем свою функцию распределения F ₁(х) = F (х, t ₁). Будем говорить, что в этом случае имеем сечение случайного процесса. Если фиксировать случайное событие w ₁ÎW, то имеем реализацию случайного процесса, то есть неслучайную функцию x ₁ = x (w ₁, t), являющейся функцией параметра t. Итак, при одном сечении процесса и одной реализации, вся информация о нем содержится в системе

Интуитивно ясно, что этой информации явно недостаточно для изучения случайного процесса.

Рассмотрим пример 3. Так как имеем случайный процесс с непрерывным временем, то при t = t ₁, случайная величина x ₁= j (w, t ₁) имеет закон распределения, представленный табл. 6.

Таблица 6

x (t 1)	x 0 (t 1)	x 1(t 1)	…	xn (t 1)	…	.
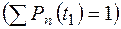P (t 1)	P 0(t 1)	P 1(t 1)	…	Pn (t 1)	…

Значения случайной величины x (t ₁): x_n (t ₁) = n, n = 0, 1, ….

Зафиксируем элементарное событие w = w_n, w_n ÎW, тогда имеем реализацию случайного процесса, или функцию одной переменной x ₁ = x ₁(t), t Î[0,¥).

Рис. 26

Рис. 26 иллюстрирует ситуацию, когда в начальный момент времени t =0 прибор находится в рабочем состоянии. При n = 1 максимальное значение x ₁(t)= Р ₁(t) равно , при n = 2 максимальное значение x ₂(t) = Р ₂(t) равно .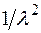

Разобранный нами случайный процесс называется пуассоновским.

Из примера видно, что изучение случайных процессов тесно связано с распределением вероятностей. Однако далеко не всегда реализация случайного процесса имеет траекторию, представляющую «вероятностную кривую» (то есть без пересечений и со значениями из [0,1]).

Пример 4. Частица совершает движение «скачком», двигаясь по перпендикулярным прямым, на бумаге в клетку, случайным образом, фиксируя свое положение в точке пересечения прямых в моменты t_i, i = 1, 2, …, n. В результате имеем достаточно сложную кривую (рис. 27). Реализация случайного процесса – траектория, описываемая параметрически парой (x ₁(t), x ₂(t)), t Î[0, Т).

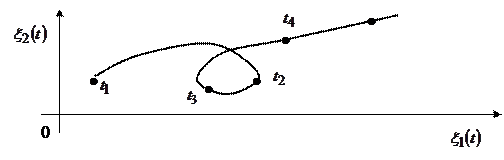
Рис. 27

Пусть имеем случайный процесс x (t)= j (w, t), тогда, при любом фиксированном t = t ₁ (по аналогии со случайной величиной), имеем закон распределения

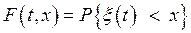. (64)

Функция (64), двух переменных, F (t, x), называется одномерным законом распределения случайного процесса x (t). Очевидно, что одномерный закон распределения не может являться достаточной характеристикой случайного процесса, поскольку он представляет только одно сечение, по которому невозможно делать выводы о всем процессе.

Ясно, что чем больше сечений, тем точнее задан случайный процесс, однако, и сложность изучения его резко возрастает. Для n сечений мы имеем функцию 2 n переменных. На практике, более чем двумерные законы используются редко.

Рассмотрим двумерный закон распределения

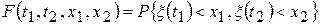, (65)

который составлен по двум сечениям процесса. Функция четырех переменных (65), оказывается, является исчерпывающей характеристикой для специального типа случайных процессов – процессов без последействия или марковских процессов (пример 3).

Марковские процессы широко используются в инженерной практике, поскольку основаны на независимости специального класса случайных событий.

Дата добавления: 2014-01-15