Марковские процессы

Понятие марковкой цепи принадлежит русскому математику А.А. Маркову (в статьях 1906-1908 гг., где он использовал новое понятие для статистического анализа распределения букв в поэме А.С. Пушкина «Евгений Онегин»). Само понятие «Цепь Маркова» было предложено русским математиком А.Я. Хинчиным.

Пусть имеем некоторую систему S, которая может находиться в одном из конечного или счетного множества несовместных состояний С_i, iÎ N. Переход системы от состояния к состоянию, вообще говоря, случаен и возможен только в фиксированные моменты времени t_n, n = 0,1,2,…. Опишем функционирование системы в терминах случайных процессов.

Пусть в момент времени t_n, система S перешла из состояния С_j в состояние С_i. Для ее описания зададим дискретный случайный процесс функцией x (t_n) = j (w_i, t_n), i = 1, 2, …; n = 0, 1, …. Элементарное событие w_i отражает пребывание системы S в состоянии C_i. Кроме того, нам необходимо задать начальное распределение вероятностей для момента времени t = t ₀ и, в общем случае, задать все сечения процесса и возможность его реализации.

Получить такую информацию о случайном процессе задача трудновыполнимая, да и в ряде случаев не нужная, если использовать понятие цепей Маркова.

В самом деле, пусть имеем последовательность (цепь) зависимых целочисленных случайных величин x_n = x (t_n), n = 0,1,…. Если в момент t_n система пришла в состояние C_i, то будем считать, что x_n = i.

Определение. Последовательность случайных величин { x_n }, n = 0,1,… образует цепь Маркова, если

,(66)

с начальными условиями

, . (67)

Вероятности 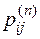- называются вероятностями перехода. Свойство (66), цепи Маркова, называется свойством отсутствия последействия, которое интерпретируется так: поведение процесса в будущем зависит только от фиксированного настоящего и не зависит от его прошлого.

Определение. Цепь Маркова { x_n }, n = 0, 1, …, называется однородной, если вероятности перехода 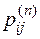не зависят от времени, то есть

, . (68)

Определение. Цепь Маркова называется неприводимой, если каждое ее состояние может быть достигнуто из любого другого, то есть для любых двух состояний системы S С_i, C_j, существует целое число к, такое, что 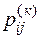> 0.

Для однородной цепи имеем > 0.

Пусть - вероятность того, что в момент времени t_n система находится в состоянии С_j. Интерес представляет существование предела

, . (69)

Нахождение распределения { p_j } является основной задачей цепей Маркова. Если предел существует, то говорят, что система S имеет стационарный режим функционирования, если . Предельные вероятности { p_j } не зависят от начальных условий, , , 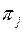означают долю времени, в течение которого система находится в состоянии С_j, j Î N, и однозначно определяются равенствами:

, (70)

, . (71)

Формула (70) называется условием нормировки.

Система алгебраических уравнений (71) является однородной, и для ее однозначного решения необходимо использовать (70), при этом, любое одно уравнение из системы (71) можно исключить.

Матрица П, составленная из элементов , называется матрицей вероятностей перехода:

. (72)

Зададим вектор вероятностей состояний системы

.

тогда система (71) записывается в виде

. (73)

Часто представляют интерес переходы системы из состояния в состояние в произвольный момент времени (переходный режим).

Для этого нужно определить распределение вероятностей пребывания системы в состоянии С_j в момент t_n. Зададим вектор вероятностей в момент t_n равенством

.

Используя (71) и определение вероятностей переходов (66), имеем

,

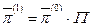где - начальное состояние системы (67). Отсюда для любого n, по рекуррентной формуле, получаем

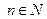, . (74)

Уравнение (74) дает общий метод вычисления вероятностей на n -м шаге процесса по заданной матрице переходов П и начальном распределении

Если стационарный режим существует, то

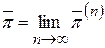. (75)

Пример. Рассмотрим систему S, которая находится, в любой момент времени t, в одном из трех состояний С ₁, С ₂, С ₃. Переход системы от состояния к состоянию происходит мгновенно в фиксированные моменты времени t _к = к, к Î N, в соответствии с размеченным графом [3] состояний рисунка 28.

Рис. 28

Требуется оценить скорость сходимости к стационарному режиму и вычислить стационарное распределение вероятностей.

Решение. Вычислим стационарное распределение вероятностей, то есть найдем собственный вектор , где , i =1, 2, 3.

Имеем 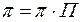, где

.

С учетом условия нормировки 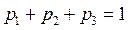имеем систему

(*)

Решая ее (например, без уравнения помеченного (*)), получаем стационарное распределение вероятностей:

.

Оценим скорость сходимости. Для этого вычислим вероятности перехода по формуле (74) при различных начальных условиях:

а) р ⁽⁰⁾ = (1,0,0),

результаты представлены в виде табл. 7.

Таблица 7

n						…
			0,250	0,178	0,203	…	0,2
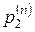
		0,75	0,062	0,359	0,254	…	0,28
		0,25	0,688	0,454	0,543	…	0,52

б) р ⁽⁰⁾ = (0,1,0),

соответствующие результаты отражены в табл. 8.

Таблица 8

n						…
			0,187	0,203	0,199	…	0,2
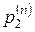
		0,75	0,375	0,250	0,289	…	0,28
		0,25	0,438	0,547	0,512	…	0,52

в) р ⁽⁰⁾ = (0,0,1),

в итоге получаем табл. 9:

Таблица 9

n						…
			0,187	0,203	0,199	…	0,2
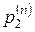
		0,75	0,313	0,266	0,285	…	0,28
		0,25	0,500	0,531	0,516	…	0,52

Из таблиц видно, что вхождение системы в стационарный режим происходит достаточно быстро, так как, уже после четырех шагов, вероятности мало отличаются от предельных, независимо от начальных условий.

Замечание. Оценка скорости сходимости переходных вероятностей к стационарным зависит от собственных значений матрицы П и иллюстрируется барицентрической системой координат [8].

Дата добавления: 2014-01-15