Непрерывные цепи Маркова

Если система с конечным или счетным числом состояний может переходить из одного состояния в другое в любой момент времени t, то будем говорить, что задана цепь Маркова с непрерывным временем.

Определение. Случайный процесс x (t) образует непрерывную цепь Маркова, если для произвольной последовательности 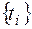, i = 1, 2, …, n, такой, что t₀ < t₁ < …< t_n, выполняется

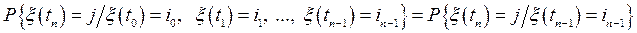. (76)

Это определение является непрерывным аналогом определения (66). Интерпретация та же самая: состояние системы S в будущем зависит только от

текущего ее состояния (настоящего) и не зависит от того, как и когда система попала в это состояние.

Определение. Цепи Маркова, сформулированные в терминах случайных процессов, называются марковскими процессами.

Рассмотренные здесь цепи Маркова - суть марковские процессы.

Непрерывные марковские процессы отличаются от дискретных тем, что случайные изменения состояний системы зависят от непрерывно изменяющихся параметров.

Пусть задан процесс x(t), определяющий состяние ситемы в момент времени tÎT. Зададим процесс ее развития: если, в данный момент времени t (t< t), система находится в состоянии i, то в последующий момент времени t она будет находится в состоянии j с вероятностью 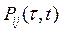, независимо от поведения системы до момента t. Для такой системы вероятности

, ,

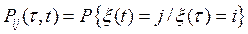называются переходными вероятностями марковского процесса.

Определение. Марковский процесс x(t) называется однородным, если переходные вероятности 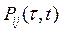зависят только от разности (t-t), то есть

.

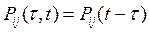В общем случае вместо переходных вероятностей можно рассматривать соответствующие плотности вероятностей. В качестве примера, можно привести броуновское движение, распространенное на непрерывный случай (Винеровский процесс [2]).

Дата добавления: 2014-01-15