Потоки событий

Потоком событий называется появление однородных событий в случайные моменты времени.

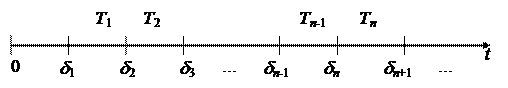
Рис. 29

Рассмотрим временную ось (рис. 29). Поток событий представляет собой, вообще говоря, последовательность случайных точек d ₁< d ₂<…< d_n на оси, разделенных временными интервалами Т_i = (d_{i +1}- d_i), i Î N, длина которых случайна.

Потоки событий различаются по законам распределения длин интервалов T_i между событиями, по их зависимости или независимости, регулярности и др.

Наиболее изучены потоки, которые обладают следующими свойствами:

а) стационарность – все его вероятностные характеристики не меняются со временем;

б) отсутствие последействия – для любых непересекающихся временных интервалов на временной оси, число событий, находящихся на одном интервале, не зависит от того, сколько их и как они оказались на другом интервале;

в) ординарность – практическая невозможность на достаточно малом временном интервале появиться двум и более событиям.

Для формализации этих свойств, введем понятие интенсивности.

Пусть 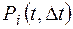- вероятность того, что за время D t, примыкающего к моменту времени t, появилось i событий, i Î N.

Рассмотрим полную группу несовместных событий, для которой, по определению, имеем

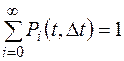. (77)

Введем обозначение, пусть 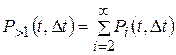- вероятность того, что за время D t появилось более одного события.

Тогда формула (77) примет вид

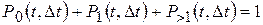. (78)

Из определения ординарности следует, что

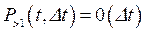, (79)

где 0(Dt) – бесконечно малая более высокого порядка, чем наименьшая из вероятносте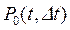й и 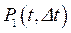, то есть .

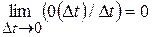Обозначим через 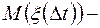математическое ожидание числа событий появившихся за время 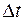, тогда, по определению,

.

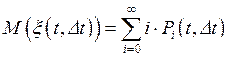С учетом ординарности и свойств бесконечно малой, имеем

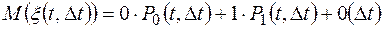
или

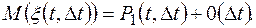
Положим

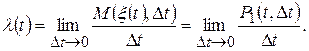
Определение. Функция 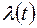параметра t называется интенсивностью (плотностью) ординарного потока событий в момент t, если

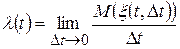. (80)

Стандартная трактовка 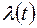- среднее число событий, приходящихся на единицу времени, для участка 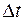, примыкающего к моменту t.

Ясно, что 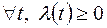, и имеет размерность обратную времени - .

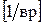Пример. Среднее число событий ординарного потока, на интервале длиной t, примыкающего к t, равно

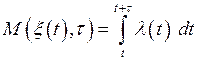, (81)

в частности, для стационарного потока, имеем

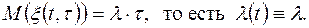
Наконец, отсутствие последействия формулируется следующим образом.

Пусть 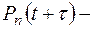вероятность того, что за время t, примыкающего к моменту времени t, появилось к событий при условии, что в момент времени t было n - к событий. Тогда условие отсутствия последействия означает, что

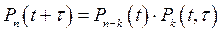, к = 0, 1, …, n. (82)

В частности, при t = D t и к = 1, имеем

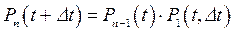. (83)

Замечание. Формула (82) в терминах биологии может интерпретироваться как вероятность роста популяции [6] на к единиц за время t. Аналогично, имеет смысл говорить о гибели популяции на к единиц за время t, если в момент t популяция состояла из (n + k) единиц, то есть

.

Определение. Поток событий называется простейшим, если он обладает свойствами:

а) стационарности: l = const,

б) отсутствия последействия:

.

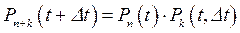в) ординарности:

.

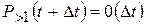Замечание. Простейший поток событий является достаточно общим, в том смысле, что получаемые вероятностные характеристики функционирования систем в условиях простейшего потока, как правило, наиболее пессимистичны, то есть «хуже не будет».

Покажем что, если поток событий простейший, то распределение длин интервалов между поступлениями любой пары соседних событий показательное (экспоненциальное) с плотностью

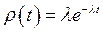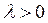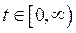, , (84)

Следующие постулаты сразу следуют из определения простейшего потока:

1) для всякого малого D t >0, существует ненулевая вероятность появления события;

2) если система начинает функционировать с момента t = 0, то первое появление события имеет место в момент t > 0.

Рассмотрим функцию

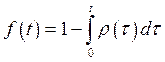. (85)

если 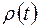- плотность, то

.

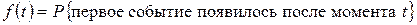Из свойства отсутствия последействия, имеем

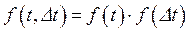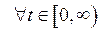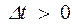, , . (86)

Вычитая из обеих частей (86) f (t), получим

.

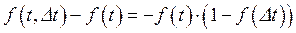Разделим обе части на D t, и перейдем к пределу по D t:

.

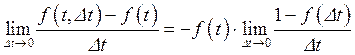Если пределы существуют, то полагая

,

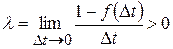будем иметь

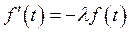, где .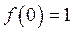

Решая это уравнение, получаем выражение

.

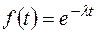Подставляя его в (84), получим

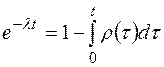
или

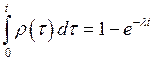. (88)

Дифференцируя (88), получаем требуемое

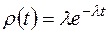._▼ (89)

Определим

.

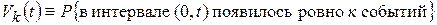Учитывая условие отсутствия последействия, можем воспользоваться сверткой

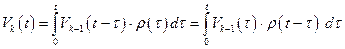, k Î N. (90)

Используя (89), имеем

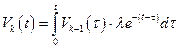. (91)

Из смысла 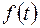и (90), при k = 0, получаем

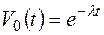. (92)

Дифференцируя (91) по t,приходим к системе уравнений

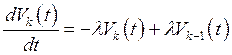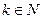, . (93)

Система рекуррентных линейных дифференциальных уравнений (93) легко решается, начиная с k = 1, если учесть (92) и начальные условия: V_к (0) = 0, k Î N. Решение системы (93) имеет вид:

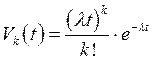, k = 0, 1, 2,.... (94)

Формула (94) представляет пуассоновский процесс (или чисто случайный процесс) с дискретным пространством состояний и непрерывным временем.

Система уравнений (93) называется системой уравнений чистого рождения [6].

Вывод. Если в некоторой системе S переходы ее из одного состояния в любое другое удовлетворяют условиям простейшего потока, то говорят, что имеет место пуассоновский процесс с непрерывным временем. Обратное также справедливо.

Пуассоновский процесс обладает некоторыми замечательными свойствами, используя которые легко получать системы уравнений вида (93), часто применяемые в системах массового обслуживания.

Дата добавления: 2014-01-15