Свойства эмпирической функции распределения

1)

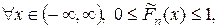
2)

3) 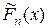имеет ступенчатый вид, непрерывна слева по определению,

4) если

5) если

Видно, что свойства эмпирической функции распределения вполне аналогичны теоретической.

Для оценки эмпирической функции распределения 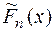теоретической 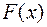используют критерий Колмогорова А.Н.

Теорема. Если функция F (x) непрерывна, то

при n ®¥,

где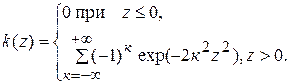

Функция 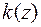называется функцией Колмогорова [2]. Её значения табулированы и приведены в приложении (табл. 5).

Замечание. Из теоремы следует, что критерий Колмогорова применим для оценки только непрерывных распределений.

Пусть требуется проверить гипотезу Н _о о том, что случайная величина x имеет своей функцией распределения непрерывную функцию F (x). Проведем n независимых испытаний и построим эмпирическую функцию 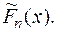Согласно теореме Гливенко [2] 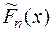есть приближение к функции .

Величина 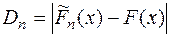есть мера отклонения Пусть 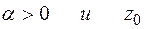такое, что , где 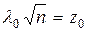. Если можно считать, что в единичном испытании практически невозможно произойти событию, вероятность которого равна a, то мы приходим к следующему критерию проверки гипотезы Н ₀ (Критерий Колмогорова).

Выдвигаем гипотезу Н ₀: F (x) – функция распределения исследуемой сл. в. x.

1) Находим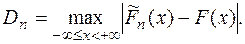

2) Вычисляем

3) По таблице находим .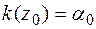

4) Если 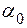достаточно велико (больше 0,2),

то гипотезу Н ₀принимаем.

Пример 1. При концентрировании молочного сырья проницаемость растворителя через мембрану является случайной величиной x, распределенной по эмпирическому закону:

.

Таблица 12

t (мин)
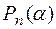
	0,135	0,26	0,36	0,45	0,518	0,57	0,628	0,648	0,735

0,78	0,72	0,83	0,85	0,875	0,892	0,91

Требуется, используя критерий Колмогорова, подобрать теоретическую функцию распределения сл. в. x при числе опытов n = 16.

Решение. Из практических соображений есть основание считать, что искомой функцией является экспоненциальное распределение:

,

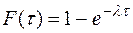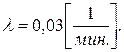
Составим таблицу значений теоретической функции распределения.

t (мин)
10^-3 F (t)

Максимальный разброс D_n при t = 55 мин. равен: , тогда 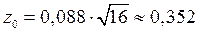. По табл. 5 приложения находим, при значение Так как a ₀ » 1 > 0,2, то гипотезу об экспоненциальности распределения проницаемости принимаем.

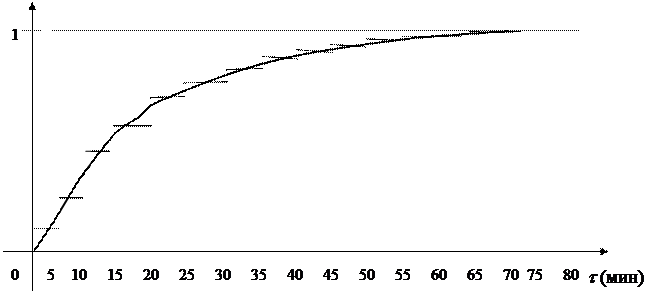Рис. 33 демонстрирует приближение эмпирической функции экспоненциальной.

Рис. 33

Критерий Колмогорова обладает наглядностью и простотой, однако, для его применения необходимо знать не только вид теоретической функции распределения, но и значения всех, входящих в неё, параметров. Заметим, что такая ситуация редко встречается на практике.

Другим критерием проверки гипотезы, о соответствии эмпирической функции распределения теоретической, является критерий c² (Пирсона).

Пусть имеем табл. 11. Требуется проверить согласование экспериментальных данных с гипотсзой о том, что случайная величина x имеет теоретическое распределение F (x).

Находим теоретические вероятности попадания случайной величины x в каждый интервал табл. 11:

р ₁, р ₂, …, р _к.

Меру расхождения c² вычисляем по формуле Пирсона [3]:

.

Распределение c² зависит от объема выборки n и числа степеней свободы r:

.

Во всех случаях имеем одно ограничение: значит, число степеней свободы 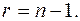Если в теоретическом распределении присутствует один параметр (например ), то число степеней свободы 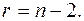Если два параметра, (например, ), то число степеней свободы 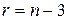и. т. д.

Зададим доверительную вероятность р. Гипотеза о законе распределения F (x) принимается, на уровне значимости р, если

.

При использовании критерия c² желательно, чтобы объем выборки был достаточно велик (n >50), а число интервалов к ³ 5.

Пример 2. Для проверки соответствия опытных данных экспоненциальному распределению примера 1, применим критерий c². Объем выборки n = 16, число степеней свободы r = 16-2 = 14. Будем считать, что число интервалов к = 16.

Взяв середину интервалов из табл. 12, получим следующую таблицу:

Таблица 13

ti	2,5	7,5	12,5	17,5	22,5	27,5	32,5
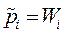
	0,135	0,125	0,1	0,09	0,068	0,082	0,048
t i× р i	0,338	0,938	1,250	1,575	1,530	2,255	1,560
37,5	42,5	47,5	52,5	57,5	62,5	67,5	72,5	77,5
0,052	0,04	0,04	0,03	0,02	0,02	0,025	0,017	0,018
1,950	1,700	1,900	1,575	1,150	1,250	1,688	1,233	1,395

Из табл. 13 находим: .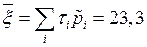

Для теоретической функции распределения , где значения вероятностей р_i найдем из формулы:

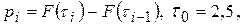
или

Результат сведем в таблицу:

t	2,5	7,5	17,5	22,5	27,5	32,5
pi	0,193	0,349	0,576	0,658	0,724	0,778
	0,0174	0,00536	0,0012	0,0024	0,0034	0,00067

37,5	42,5	47,5	52,5	57,5	62,5	67,5	72,5	77,5
0,821	0,855	0,884	0,906	0,924	0,949	0,951	0,960	0,968
0,019	0,001	0,0051	0,0024	0,00022	0,0017	0,0014	0,00071	0,00125

Составим сумму

= 16 × 0,0829 = 1,326.

Зададим доверительную вероятность р =0,95.

По таблицам приложения (табл. 6), при n - r = 16 – 2 = 14 степеней свободы, определяем значение c² = 23,7,а так как 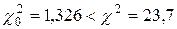, то с вероятностью р = 0,95 гипотеза, о соответствии эмпирической функции теоретической, принимается.

Упражнение. Решить пример для случая, когда число интервалов к = 8.

Замечание. В предлагаемых примерах соответствие настолько хорошее, что вызывает сомнение в том, что эмпирические данные не подтасованы. В практических приложениях уже при R ³ 0,3 гипотезу можно считать правдоподобной, тем более, если критерий Колмогорова дает аналогичный результат.

Замечание. Следует заметить, что для критерия Колмогорова параметр l =0,03 взят интуитивно, а для критерия c², он получен по опытным данным. Если бы мы для поверки гипотезы использовали бы l = 0,03 в критерии c², то соответствие было бы еще лучше. Следовательно, можно поставить задачу о нахождении интервала допустимых значений параметра l, которая рассматривается ниже.

Как видно, для применения критерия Пирсона, необходимо иметь достаточно большой объем выборки, да и его использование, по сравнению с критерием Колмогорова, достаточно громоздко. Тем не менее, применение критерия Пирсона обладает тем преимуществом, что числовые значения параметров теоретической функции распределения можно получить из имеющейся выборки, то есть заранее нам достаточно знать только общий вид теоретической функции распределения, причем любой случайной величины. Критерий Колмогорова в этом смысле более жесткий. Желательно при проверке гипотезы о соответствии теоретической функции распределения эмпирическим данным, применять оба критерия.

Задача нахождения теоретической функции распределения требует проведения достаточно большого числа опытов, а также, по крайней мере, общего вида искомой функции. Такая ситуация далеко не всегда встречается на практике.

Чаще всего имеется выборка относительно малого объема или вид теоретической функции распределения неизвестен.

В этом случае обычно вычисляют числовые характеристики случайных величин (моменты, вероятности и т. д.).

4.2 Точечные оценки неизвестных параметров законов распределения

Здесь мы рассматриваем задачи определения неизвестных параметров законов распределения случайных величин в условиях относительно малых объемов эмпирических данных. Ясно, что каким бы не был объем выборки, значение параметра, который мы оцениваем, будет приближенным. Это приближение называется оценкой параметра. Для того чтобы оценка была наилучшей, требуется иметь о ней наиболее полное представление.

Пусть случайная величина x распределена по закону, который содержит неизвестный параметр 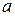. Требуется найти для него подходящую оценку 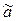по результатам выборки:

. (122)

При выборе условий, налагаемых на оценку неизвестного параметра прежде мы должны построить математическую модель эксперимента. Под этим мы понимаем следующее:

1) выборка (122) является n –мерным случайным вектором

где случайные величины определены на одном и том же пространстве элементарных событий и имеют, соответственно, одну и ту же функцию распределения и, тем самым, одни и те же параметры;

2) выборка (122) репрезентативна, то есть любой элемент пространства элементарных событий имеет одинаковую вероятность попасть в выборку.

Таким образом, оценка параметра 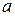есть n –мерная неслучайная функция n случайных аргументов

.

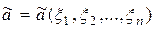Принято считать, что оценка должна удовлетворять условиям

а) несмещенности:

практически это означает, что систематические ошибки отсутствуют;

б) эффективности, то есть оценка более эффективна чем 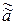, если

эффективность оценки означает, что её дисперсия меньше, чем дисперсия других оценок;

в) состоятельности, то есть

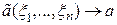при

состоятельность означает, что для оценки выполняется закон больших чисел (теорема Чебышева или её следствия, см. раздел 3).

Замечание. Напрактике не всегда удается удовлетворить всем этим требованиям по соображениям объективного или экономического характера. Тем не менее, желательно пытаться исследовать оценку на достоверность.

Дата добавления: 2014-01-15