Модификация основных параметров ГА

Модификации оператора селекции:

1. На основе рулетки.

Каждой хромосоме соответствует своя зона (сектор) рулетки.

2. На основе заданной шкалы.

Сначала вся популяция упорядочивается, затем каждой хромосоме ставится в соответствие определённое число, например, значение функции нормализованного фитнесса:

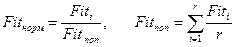, где r – число членов популяции

3. Элитная селекция.

Вся популяция упорядочивается по значениям функции фитнессаи затем выбирается k лучших хромосом, которые скрещиваются. Этот способ может привести к преждевременной сходимости, поэтому наряду с элитной селекцией применяется механизм «встряхивания» (то есть убирается l лучших хромосом, а на их место ставятся l худших или случайных).

4. Турнирная селекция.

Выбирается k лучших хромосом, среди них осуществляется скрещивание.

5. Схема рекомбинации.

Заключается в использование хромосом, значительно отличающихся друг от друга.

Модификации оператора кроссинговера:

1. Многоточечный кроссинговер.

H1	0 0 1 1 0 1 0 1
H2	1 0 1 0 1 0 1 0
H1^’	0 0 1 0 0 1 1 0
H2^’	1 0 1 1 1 0 0 1

H1	0 0 1 1 0 1 0 1
H2	1 0 1 0 1 0 1 0
H1^’	0 0 1 0 1 0 1 0
H2^’	1 0 1 1 0 1 0 1

Замечание. Не рекомендуется применять большое число точек разрезания, так как это может привести к потере нужных свойств.

2. Порядковый кроссинговер.

3. Частично соответствующий кроссинговер:

1. точка кроссинговера выбирается случайно.

2. производится анализ соответствия сегментов первого и второго родителя.

4. Циклический кроссинговер.

При решении задач комбинаторной оптимизации стоит проблема нахождения допустимого решения.

H₁ 1 2 3 4 5 6 7 8 9 10

H₂ 5 3 9 1 4 8 10 2 6 7

Формируют пути, которые позволяют установить соответствие между генами двух рассматриваемых хромосом.

I. (1,5), (5,4), (4,1)

II. (2,3), (3,9), (9,6), (6,8), (8,2)

III. (7,10), (10,7)

H^/ 5 3 9 1 4 8 10 2 6 7

5. Универсальный кроссинговер.

Точка кроссинговера не указывается, а задается маска, которая участвует в получении хромосом.

H₁ 0 1 1 0 0 1

H₂ 0 1 0 1 1 1

маска 0 1 1 0 1 0 → случайным образом с вероятностью 0.5

H₁^/ 0 0 0 0 1 1

H₂^/ 0 0 1 1 0 1

6. «Жадный» кроссинговер.

За один эксперимент находится лучшее решение:

1. для всех хромосом вычисляется значение функции фитнесса;

2. на одной из хромосом выбирается точка кроссинговера и для i -го гена (слева от *) вычисляется значение частичной функция Fit, то есть стоимость пути от i -го гена до рядом стоящего, затем – аналогично для всех хромосом;

3. от потомка берется тот ген, для которого функция Fit наилучшая.

	a	b	c	d	e
a	–	15	6	7	8
b	15	–	4	3	2
c	6	4	–	1	10
d	7	3	1	–	9
e	8	2	10	9	–

P={H₁,H₂,H₃}

H₁ = abcde

H₂ = bdeca

H₃ = ebadc

b→c H₁ Fit = 4

b→a H₁ Fit = 15

b→d H₁ Fit = 3

H₁^/=bdcae (Fit = 18 )

H₂^/= 28

H₃^/= 25

Дата добавления: 2014-01-15