
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Динамическое изменение параметров в процессе выполнения ГА
|
|
|
|
Еnd.
End while
While not termination do
Begin
Мобильные ГА
В мобильных ГА длина хромосома может быть переменной (имеют дело со строками переменной длины). Строки могут быть переопределены (хромосома несёт избыточную информацию) или недоопределены (хромосома другой информацией).
В мобильных ГА используются два дополнительных оператора:
· Cut (разрезание)
· Splice (сцепление)
<номер гена: значение гена>
t =0; //начальный момент времени эволюции
init_population (Prt); // инициализация популяции
// r – число хромосом, t - время
pp_preparing-population; // насыщение популяции
prp; //селекция хромосом
prcr = cut or splice (prs); //разрезание
prm = mutation (prcr); // мутация
pt+1 =gen (p p, prcr, prm);
t=t +1;
Отличия мобильного ГА от классического ГА:
1. Используются специальные операторы cut и splice вместо оператора кроссинговера, оперирующего хромосомами фиксированной длины.
2. Возможность формирования хромосом в популяции на каждом этапе оптимизации.
3. Генетическое разнообразие мобильного ГА значительно выше, поскольку в процессе эволюции может изменяется позиционирование генов внутри хромосом.
Несмотря на успешное использование ГА в большом количестве задач оптимизации, универсальных методов построения и настройки ГА в настоящее время не существует. Холланд и Голдберг разработали фундаментальные основы ГА, вывели и доказали теорему схем, которая отражает основные механизмы работы ГА и даёт качественную картину того, как ГА мог бы работать.
Схема (шаблон) – описывает набор строк (подмножество всех возможных строк) с подобными значениями в некоторых позициях. Схема представляет собой строку длиной l, состоящую из символов алфавита {0, 1, *}.
Пример: 0*10 = {0010, 0110}
Введение схемы позволяет компактно представить похожие хромосомы. Это позволяет концентрировать в области скопления похожих хромосом островки решений. Островки образуют область решений.
каждая строка, представленная схемой, называется примером схемы.
Фиксированные позиции в схеме – позиции, в которых находятся 0 или 1.
Для каждой схемы определяется два параметра:
- порядок схемы
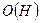 – определяется количеством фиксированных позиций в схеме;
– определяется количеством фиксированных позиций в схеме; - длина схемы
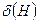 – расстояние между самыми дальними фиксированными позициями.
– расстояние между самыми дальними фиксированными позициями.
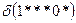
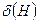 =4
=4
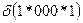
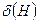 =6
=6
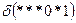
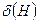 =2
=2
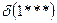
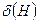 =0
=0
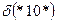
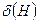 =1
=1
Теорема схем:
Схемы малого порядка, малой длины и с приспособленностью выше средней получают в очередных поколениях экспоненциально увеличивающиеся число представителей.
Использование оператора кроссинговера приводит к меньшему разрушению схем с малой длиной. Это позволяет сохранить представительство хромосом, соответствующих данной схеме, в следующих поколениях.
Оператор мутации реже разрушает схемы с низким порядком.
Холланд доказал, что если ГА явным образом обрабатывает n строк в каждом поколении, то в то же время не явным образом, использую строительные блоки, он обрабатывает n 3 строк с высокой функцией фитнесса.
Строительные блоки – схемы с высокой функцией фитнесса, короткой длиной и малым порядком.
Запись теоремы схем в формальном виде:
m (H, t) – число представителей схемы H на шаге t.
Вычислим ожидаемое число представителей схемы H в следующем поколении (на шаге t +1) m (H, t +1):
Каждой схеме ставится в соответствие значение вероятности её выживания в следующем поколении:

где fit (H) – приспособленность данной схемы;
fitср – средняя приспособленность в данной популяции.
Вероятность того, что схема не будет разрушена оператором кроссинговера, равна:
 , где l – количество бит в строке.
, где l – количество бит в строке.
Схема не будет разрушена, если в операции скрещивания участвуют похожие хромосомы.
Схема переживёт мутацию, если выполняется условие:
 .
.
Формальное описание теоремы схем:
 .
.
Выводы:
1. Значения функций приспособленности fit (H) и fitср изменяются в процессе эволюции, поэтому чем больше отношение 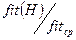 , тем больше вероятность попадания схемы в популяцию.
, тем больше вероятность попадания схемы в популяцию.
 мера давления отбора.
мера давления отбора.
2. Увеличение значений 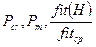 приводит к расширению пространства поиска, но не к увеличению количества хороших схем. С уменьшением значений
приводит к расширению пространства поиска, но не к увеличению количества хороших схем. С уменьшением значений 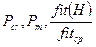 увеличивается использование хороших схем, но тормозится исследование пространства. Поэтому необходимо соблюдать баланс между пространством используемых схем и пространством поиска.
увеличивается использование хороших схем, но тормозится исследование пространства. Поэтому необходимо соблюдать баланс между пространством используемых схем и пространством поиска.
3. Теорема схем даёт качественную картину функционирования ГА, снабжает разработчика знаниями о хороших способах кодирования, реализации и применении операторов ГА.
4. Теорему схем трудно применить к конкретным вариантам ГА с целью количественного анализа динамики работы и выбора его параметров. Теорема схем даёт лишь нижнюю границу ожидаемого количества представителей схемы в популяции на следующем шаге алгоритма, поэтому теорему нельзя использовать для прогнозирования развития ГА на несколько шагов вперёд.
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 347; Нарушение авторских прав?; Мы поможем в написании вашей работы!