Устойчивость объектов и систем уравнения

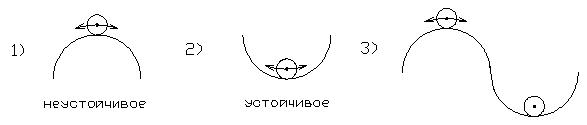Методы оценки устойчивости объектов и систем:

1) Корневой (критерий Ляпунова)

Для корневой устойчивости линейной системы необходимо и достаточно, чтобы все корни характеристического полинома ее передаточной функции имели отрицательные вещественные части.

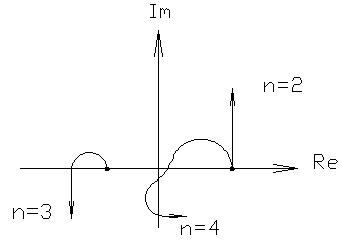
1 – устойчивые корни

2 – нулевой корень

3 – нейтральные корни

4 – неустойчивые корни

Качественная оценка характеристического полинома.

Необходимое условие устойчивости всех корней характеристического полинома:

1) Все корни характеристического полинома должны быть одного знака;

2) Характеристический полином должен быть полным, т.е. содержать все нулевые коэффициенты, т.е. для каждого , .

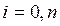Эти же условия для полинома второго порядка являются и достаточными, а для полиномов более высокого порядка они только необходимые.

Все методы оценки устойчивости делятся на 2 основных класса:

а) Алгебраические (с помощью алгебраических вычислений)

б) Частотные (используя частотные характеристики)

Алгебраический критерий:

1) Раусса

2) Гурвица

3) Льенара-Шипара

1) В 1878 английский математик Раус предложил критерий:

Исходными данными является характеристический полином

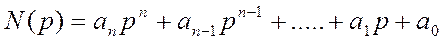
По критерию Раусса исследуемая система устойчива, если все коэффициенты в первом столбце таблицы Раусса имеют одинаковый знак, если условие не соблюдается, то характеристический полином имеет неустойчивые корни. Количество которых равно числу перемен знака. В таблице всегда (n-1) строк.

2) В 1895 году изобрел новый критерий немецкий математик Гурвиц.

Для оценки устойчивости также используется характеристический полином. На его основе составлен главный определитель Гурвица.

=

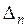Для проверки правильности составления определителя, анализируется главная диагональ, там должны стоять все коэффициенты характеристического полинома от 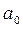до .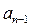

Правило определения устойчивости: Если все диагональные миноры положительны и 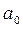тоже, то данный объект является устойчивым, если главный минор равен 0, то либо 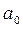=0 и есть один нулевой корень, либо другие коэффициенты равны 0 и есть пара чисто мнимых корней.

3) Правило: Если все коэффициенты характеристического полинома равны 0 и все главные миноры матрицы Гурвица с четными (нечетными) номерами тоже, то характеристический полином является устойчивым.

б) Частотный критерий - Критерий устойчивости Михайлова.

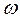Основывается на построении на комплексной плоскости кривой, которая вычерчивает вектор характеристического полинома при изменении от 0 до 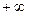, она называется годографом Михайлова.

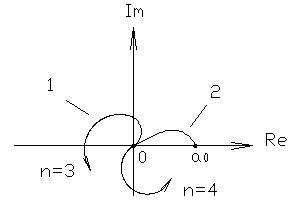
Правило оценки устойчивости: Для того, чтобы система была устойчива необходимо и достаточно, чтобы годограф начинался на положительной вещественной оси из точки 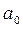и последовательно против часовой стрелки проходил количество квадрантов, равное размерности системы или степени характеристического полинома.

Пример: Устойчивые

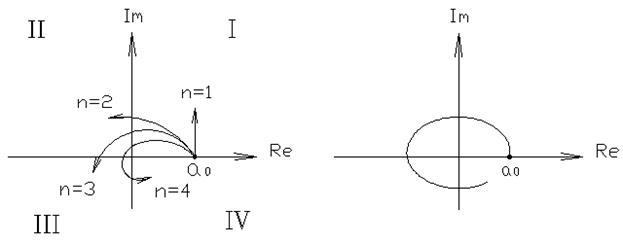Пример: неустойчивые

Пример: на границе устойчивости

Дата добавления: 2014-01-15