Закон полного тока в интегральной форме

Пусть поверхность S, ограниченная контуром l, пронизывается токами I ₁, I ₂,… I_n (рис. 4.8). Для любой среды . Проинтегрируем это равенство по поверхности S

.

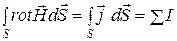Заменим левую часть равенства по теореме Остроградского-Стокса, получим

, (4.21)

где - алгебраическая сумма токов, сцепленных с контуром интегрирования.

Полученное равенство носит название закона полного тока:

циркуляция вектора 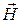по замкнутому контуру равна сумме токов, пронизывающих этот контур, и не зависит от формы и величины контура.

Этот закон позволяет легко рассчитать симметричные поля, например, поля с осевой и цилиндрической симметрией, когда напряженность поля в каждой точке поля одинакова и может быть вынесена за знак интеграла, а интеграл приводится к простейшему виду.

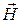Циркуляцию вектора по аналогии с электродвижущей силой называют магнитодвижущей силой.

Если контур интегрирования L ₁ (рис. 4.9) не охватывает проводник, по которому течет постоянный ток, то в этом случае , а значит , т.е. контур расположен в потенциальной области поля.

Для замкнутого контура L ₂ циркуляция вектора 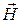не равна нулю, т.к. контур интегрирования охватывает проводник с током I, который является вихревой областью, и в нем .

Для контура интегрирования L ₃ алгебраическая сумма токов, пронизывающих этот контур, равна нулю, поэтому .

Если ток протекает по катушке с числом витков w и контур интегрирования пронизывает все витки (рис. 4.10), то закон полного тока примет вид

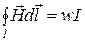. (4.22)

Расчет поля в этом случае по закону полного тока невозможен, ибо в различных точках контура интегрирования напряженность поля различная, и ее нельзя выносить за знак интеграла. В этом случае для расчета поля можно воспользоваться формулами для вектора магнитной индукции или вектор-потенциала.

Пример. Пусть магнитное поле создается постоянным током I, протекающим по бесконечно длинному проводнику (рис. 4.11). Определим напряженность магнитного поля в точке, расположенной вне провода на расстоянии а от его оси. Проведем контур l вокруг провода, тогда согласно закону полного тока,

.

Но векторы 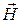и совпадают по направлению, поэтому .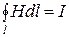

Поле, создаваемое током, протекающим по бесконечному проводу, симметрично, т.е. на одинаковом расстоянии от оси провода в плоскости, перпендикулярной проводу, величина Н одинакова. Поэтому ее можно вынести за знак интеграла

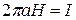, откуда 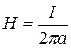и 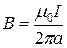. (4.23)

Дата добавления: 2014-01-15