Принцип метода расчета с учетом неравномерности движения поездов

Основные положения этого метода разработаны отечественными учеными, они рассмотрены в работах [1, 7].

Число поездов в фидерной зоне случайно из-за случайного их расположения в зоне питания и непрерывного движения, это число является основным фактором, определяющим нагрузку в системе тягового электроснабжения.

Любая случайная величина наиболее полно характеризуется законом ее распределения, который определяет вероятность нахождения в фидерной зоне (зоне питания) конкретного числа поездов.

4.4.1. Законы распределения числа поездов

Из всего многообразия законов распределения случайных величин при рассмотрении распределения числа поездов наиболее часто используются
два – биноминальный и гипергеометрический.

Биноминальный закон распределения соответствует случаю, когда рассматривается повторение одного и того же опыта при постоянных условиях, причем в качестве элементарных исходов каждого отдельного опыта различают два: появление некоторого события А и непоявление этого события А.

Таким образом, можно предполагать независимость появления поездов, т. е. появление одного поезда в зоне не изменяет вероятности появления любого другого.

Примем следующие обозначения: n – максимальное число ниток графика движения поездов; m – число ниток графика, занятое поездами; (n – m) – число ниток, свободное от поездов; А – событие, что m любых ниток занято поездами; В – событие, что (n – m) свободных ниток; А₁, А₂, А_m – события, что первая, вторая, m-я нитки заняты поездами; В₁, В₂, В_(n-m) – события, что первая, вторая, (n – m)-я нитки свободны; М₁ – событие, что m ниток занято, а (n – m) – свободно.

Согласно теории вероятности можно записать:

;

(4.17)

.

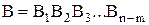(4.18)

По аналогии с выражениями (4.17) и (4.18) запишем:

.

(4.19)

Поскольку при биноминальном законе события А_j и В_j независимы, можно записать, что вероятности каждого события будут одинаковы, т. е.

;

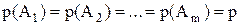(4.20)

.

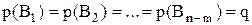(4.21)

Вероятность того, что в данной комбинации будет m ниток занято поездами, а (n – m) ниток будет свободно, определяется как

,

(4.22)

или

,

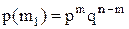(4.23)

где m₁ – число поездов одной комбинации.

Возможное число комбинаций поездов и ниток равно числу сочетаний:

.

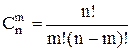(4.24)

Вероятность любой возможной комбинации из m поездов в n нитках графика

.

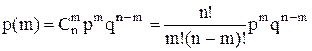(4.25)

Максимальное число поездов за время Т обозначим N₀. Фактически имеем N. Следовательно, можно записать:

;

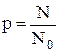(4.26)

.

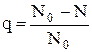(4.26`)

Тогда

.

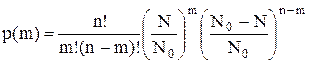(4.27)

При биноминальном законе распределение вероятностей соблюдается условие:

.

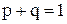(4.28)

Гипергеометрический закон распределения числа поездов основан на вероятности появления поездов взаимозависимо.

Необходимо знать вероятность того, что за время t будет отправлено m поездов или в n нитках (внутри периода t) расположится m поездов.

Пусть все поезда в графике сохраняют свою последовательность по времени. Допустим, что поезд с номером k, лежащий между поездами с номерами k – 1 и k+1, может располагаться на любой свободной нитке между этими поездами (не выходя за их пределы). Если принять такое допущение и для остальных поездов, то можно подсчитать число графиков, которое можно составить, изменяя положение m поездов в n нитках (внутри интервала времени t). Очевидно, оно будет равно числу сочетаний из n по m, т. е. .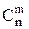

Подобным же образом можно передвигать поезда в свободных нитках между парой других смежных поездов и за пределами рассматриваемого интервала времени. Число таких графиков движения будет равно .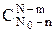

Следовательно, общее число графиков движения, удовлетворяющих условию, что в интервале t будет m поездов, можно определить как

.

(4.29)

Если же позволить всем поездам занимать любые смежные свободные нитки, то всего можно было бы построить 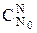графиков.

Вероятность графика, удовлетворяющая искомому условию (m поездов в интервале t),

.

(4.30)

В теории вероятности подобная зависимость носит название гипергеометрического распределения.

Используя теоретические законы распределения числа поездов, можно вычислить показатели системы тягового электроснабжения через числовые характеристики, полученные для этих законов.

4.4.2. Средние значения расчетных показателей

системы тягового электроснабжения

Для любой расчетной величины А ее среднее значение 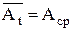равно математическому ожиданию М(t) мгновенного значения А_t.

Средние токи поездов могут рассматриваться как математическое ожидание от мгновенных токов.

Средние токи фидеров, плеч питания, тяговых подстанций следует рассматривать как математическое ожидание мгновенных значений таких токов. Эффективные токи фидеров, плеч питания, тяговых подстанций находятся также через математические ожидания от квадрата мгновенных значений.

Средние потери напряжения до поезда и средние потери мощности можно рассматривать как математические ожидания от мгновенных значений этих величин.

В качестве примера рассмотрим схему одностороннего питания поездов (рис. 4.5).

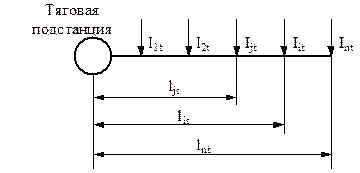
Рис. 4.5. Схема одностороннего питания поездов

Мгновенное значение потери напряжения при одностороннем питании тяговой сети до поезда i согласно выражению (4.10)

.

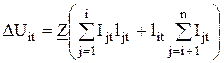(4.31)

Считая, что средняя потеря напряжения за время хода поезда по перегону равна математическому ожиданию от мгновенных значений потерь напряжения, запишем:

.

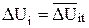(4.32)

Подставив в формулу (4.32) выражение (4.31), получим:

.

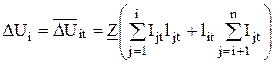(4.33)

Рассмотрим модель биноминального закона распределения числа поездов, т. е. будем считать поезда на перегонах независимыми.

Нагрузка поезда теоретически зависит от его расстояния до подстанции за счет потери напряжения в тяговой сети. Все случайные величины l_j, I_j в выражении (4.33) независимы. Тогда согласно теореме о математическом ожидании суммы и произведения независимых случайных величин можно записать:

,

(4.34)

где 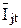– средний ток (математическое ожидание), потребляемый поездами на перегоне j за расчетный период Т; , 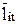– средние расстояния от поездов j, i до подстанции.

Пусть график потребления тока будет таким, как это показано на рис. 4.6.

Рис. 4.6. Токи поездов:
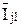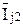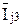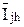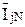, , , , – средние токи поездов 1, 2, 3, …h…, N

за время их хода по перегону j

Средний ток перегона за время Т

,

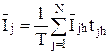(4.35)

где t_jh – время хода по перегону j поезда h.

Умножив и разделив правую часть выражения (4.35) на U, его можно
записать в виде:

,

(4.36)

где W_jh – энергия, потребляемая поездом h на перегоне j; W_jT – энергия, потребляемая всеми поездами на перегоне за время Т.

Наличие вычислительной техники позволило создавать методы, где расчетные формулы могли бы быть использованы как алгоритм для ЭВМ. К ним можно отнести метод наложения, матричные методы расчета [2, 3], имитационное моделирование [4] и др.

Выбор метода расчета той или иной из рассмотренных величин для определения параметров системы электроснабжения или определения условий ее работы при заданных параметрах определяется исходными условиями и характером определяемой величины.

5. ВЫБОР ПАРАМЕТРОВ СИЛОВОГО ОБОРУДОВАНИЯ

ТЯГОВЫХ ПОДСТАНЦИЙ И СЕЧЕНИЯ ПРОВОДОВ

КОНТАКТНОЙ СЕТИ

Расчет системы тягового электроснабжения представляет собой технико-экономическую задачу, при решении которой намечается размещение тяговых подстанций, определяется их мощность, производится выбор типа и числа агрегатов; принимается схема питания и секционирования контактной сети, производится расчет сечения контактной подвески; выбираются и рассчитываются схема внешнего электроснабжения, защита от токов короткого замыкания.

Результаты расчета системы тягового электроснабжения позволяют выполнить комплексный проект электрификации железной дороги, где определяются объемы и методы строительно-монтажных работ.

Дата добавления: 2014-01-15