
- Р Р‡.МессенРТвЂВВВВВВВВжер
- ВКонтакте
- РћРТвЂВВВВВВВВнокласснРСвЂВВВВВВВВРєРСвЂВВВВВВВВ
- РњРѕР№ Р В Р’В Р РЋРЎв„ўР В Р’В Р РЋРІР‚ВВВВВВВВРЎР‚
- LiveJournal
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Анализ цепи с идеальным индуктивным элементом
|
|
|
|
Индуктивная катушка с активным сопротивлением RL = 0 называется идеальной. Подключим к идеальной катушке индуктивности источник синусоидального напряжения, что проиллюстрировано на рис. 6.3.
Под воздействием приложенного синусоидального напряжения по виткам катушки будет протекать ток. Примем начальную фазу тока равной нулю, то есть:
iL = ImLsin ωt. (6.11)
 |
Из рис. 6.3 и выражения (6.1) следует, что мгновенное значение напряжения на индуктивности определяется скоростью изменения тока
 . (6.12)
. (6.12)
Выражение (6.12) с учетом формулы (6.11) после дифференцирования примет вид:
 , (6.13)
, (6.13)
где UmL = Lω·ImL – амплитуда падения напряжения на идеальной индуктивности.
Из выражения (6.13) найдем значение амплитуды тока:
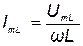 . (6.14)
. (6.14)
В формулах (6.13) и (6.14) величина ωL имеет размерность сопротивления, а именно: 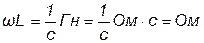 , и носит название индуктивного сопротивления. Обозначается индуктивное сопротивление ХL = ωL = 2π·f·L. Величина, обратная индуктивному сопротивлению, называется индуктивной проводимостью. Индуктивное сопротивление является реактивным, так как характеризует способность элемента создавать ЭДС самоиндукции, противодействующую протеканию переменного тока в цепи. Отметим, что в цепи постоянного тока ω = 0 и ХL = 0.
, и носит название индуктивного сопротивления. Обозначается индуктивное сопротивление ХL = ωL = 2π·f·L. Величина, обратная индуктивному сопротивлению, называется индуктивной проводимостью. Индуктивное сопротивление является реактивным, так как характеризует способность элемента создавать ЭДС самоиндукции, противодействующую протеканию переменного тока в цепи. Отметим, что в цепи постоянного тока ω = 0 и ХL = 0.
Для построения векторной и временной диаграмм, а также для сравнения фаз тока и напряжения запишем выражение (6.14) в синусоидальной форме:
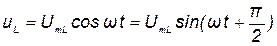 . (6.15)
. (6.15)
Сравнивая выражения (6.11) и (6.15) для мгновенных значений тока и напряжения можно сделать вывод, что в цепи с идеальной индуктивной катушкой напряжение опережает ток по фазе на угол 900 (π/2).
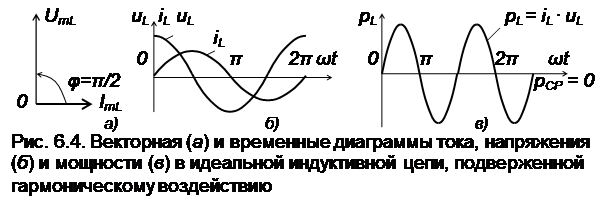 Векторная и временная диаграммы тока и напряжения в цепи с идеальной катушкой индуктивности проиллюстрированы на рис. 6.4.
Векторная и временная диаграммы тока и напряжения в цепи с идеальной катушкой индуктивности проиллюстрированы на рис. 6.4.
Из рис. 6.4, в следует, что мгновенное значение мощности определяется произведением мгновенных значений напряжения и тока:
pL = uL ·iL =UmLcosωt·ImLsinωt = UmL·ImLcosωt·sinωt. (6.16)
Правую часть уравнения (6.16) умножим и разделим на 2. Тогда получим:
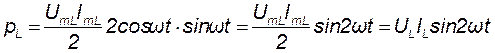 . (6.17)
. (6.17)
Из выражения (6.17) видно, что мгновенная мощность в цепи с идеальной индуктивностью изменяется с двойной частотой по сравнению с частотой изменения тока и напряжения в этой же цепи.
В цепи с идеальной катушкой индуктивности происходит непрерывное колебание (обмен) энергии WL между магнитным полем этой катушки индуктивности и энергией источника. Максимальное значение (пик) магнитной энергии равно:
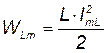 .
.
Амплитудное значение мгновенной мощности или произведение действующих значений напряжения и тока в цепи с индуктивностью называется реактивной индуктивной мощностью или просто индуктивной мощностью:
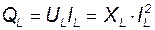 , вар. (6.18)
, вар. (6.18)
В формуле (6.18) «вар» означает вольт-ампер реактивный.
Отметим, что среднее значение мощности рСР = 0 в цепи с идеальной индуктивностью за период Т равно нулю, что показано на рис. 6.4, в.
6.2.3. Анализ цепи с ёмкостным элементом
Подключим (рис. 6. 5) к источнику переменного тока конденсатор С, токами утечки которого пренебрегаем ввиду их малости
 |
Принимаем, что напряжение источника изменяется по синусоидальному закону с нулевой начальной фазой, и мгновенное значение напряжения на обкладках конденсатора С равно:
uC = u = UmCsin ωt. (6.19)
Из курса физики известно, что заряд на обкладках конденсатора определяется выражением:
q = C·u = C·UmCsin ωt. (6.20)
Сравнивая выражения (6.19) и (6.20) заключаем, что закон изменения заряда тот же самый, что и закон изменения напряжения. Скорость изменения заряда конденсатора во времени или то же самое, что скорость изменения напряжения, будет определять ток в цепи:
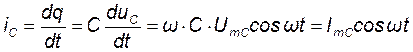 . (6.21)
. (6.21)
В выражении (6.21) ImC = ω·C·UmC величина ω·C имеет размерность проводимости (сименс) и называется реактивной ёмкостной проводимостью. Величина, обратная проводимости является реактивным ёмкостным сопротивлением или просто ёмкостным сопротивлением:
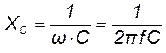 , Ом.
, Ом.
Для построения векторной и временной диаграмм, а также для сравнения фаз тока и напряжения запишем выражение (6.21) в синусоидальной форме:
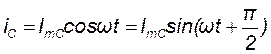 . (6.22)
. (6.22)
Сравнивая выражения (6.19) и (6.22) для мгновенных значений тока и напряжения можно сделать вывод, что в цепи с конденсатором ток опережает напряжение по фазе на угол 900 (π/2).
Векторная и временная диаграммы тока и напряжения в цепи с ёмкостным элементом проиллюстрированы на рис. 6.6.
|
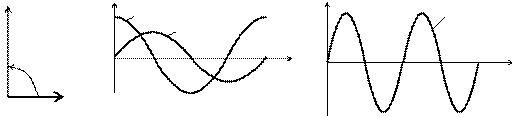 |
Из рис. 6.6, в следует, что мгновенное значение мощности определяется произведением мгновенных значений напряжения и тока:
pС = uс ·iС =ImCcosωt·UmCsinωt = UmC·ImCcosωt·sinωt. (6.23)
Правую часть уравнения (6.23) умножим и разделим на 2. Тогда получим:
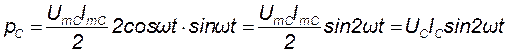 . (6.24)
. (6.24)
Из выражения (6.24) видно, что мгновенная мощность в цепи с конденсатором изменяется с двойной частотой по сравнению с частотой изменения тока и напряжения в этой же цепи.
В цепи с идеальным конденсатором происходит непрерывное колебание (обмен) энергии WС между электрическим полем этого конденсатора и энергией источника. Максимальное значение (пик) электрической энергии равно:
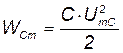 .
.
Как и в цепи с идеальной индуктивной катушкой, цепь с ёмкостным элементом не потребляет мощность от источника, то есть в этих цепях происходит полный обмен энергией без потерь между источником и цепью.
Амплитуда колебаний мгновенной мощности в цепи с ёмкостью называется реактивной ёмкостной мощностью или просто ёмкостной мощностью:
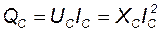 , вар.
, вар.
Таким образом, рассмотрены законы Ома и Кирхгофа для переменного тока, а также проанализированы электромагнитные процессы в R, L и С цепях переменного тока.
Тест 14
Гармоническое воздействие на элементы R, L и С электрической цепи
Для каждого п. 1- 4 теста запишите номера только соответствующих ему позиций
| Элемент цепи | Положение вектора модуля падения напряжения на элементе | Величина фазового сдвига между током и напряжением | Соотношение между действующими значениями тока и напряжения | Среднее значение | |
| Мгновенной мощности | Энергии | ||||
| 1. Резистор 2. Ёмкость 3. Индуктивность. 4. Проводимость. | 5. Отстает от тока 6. Опережает ток 7. Совпадает с током | 8. π/2 9. 0 10. - π/2 | 9. 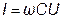 10.
10. 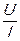 , 11. , 11.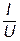 12.
12. 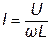 13.
13. 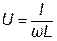 14.
14. 
| 15. U·I 16. 0 | 17. 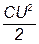 18.
18. 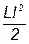 19. U·I· t
19. U·I· t
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 1902; Нарушение авторских прав?; Мы поможем в написании вашей работы!