
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Изображении
|
|
|
|
Лекция 8. Анализ цепей переменного тока в комплексной форме
Воздействии
Тема 2. Анализ линейных цепей при гармоническом
Комплексные числа
Для каждого п. 1- 4 теста запишите номера только соответствующих ему позиций
| Форма записи комплексного числа | Составляющие части комплексного числа | Модуль | Аргумент | Оператор вращения | |
| вещественная | мнимая | ||||
| 1. Алгебраическая. 2. Геометрическая. 3. Тригонометрическая 4. Показательная. | 5. Cosα 6. Нет 7. А’ 8. Re[A] | 9. Jm[A] 10. jSinα 11. Hет 12. jA’’ | 13. Длина вектора. 14. Амплитуда гармоники, равная единице. 15. Постоянный коэффициент. 16. Квадратный корень суммы квадратов вещественной и мнимой частей | 17. Величина отношения мнимой к вещественной части. 18. Угол наклона вектора. 19. Величина отношения вещественной к мнимой части. 20. Начальная фаза (фаза). 21. еjα | 22. Нет 23. Есть |
8.1. Представление R, L и С элементов в комплексном
Комплексные ток и напряжение резистивного элемента (сопротивления) имеют одинаковые аргументы и отличаются по модулю в R раз, в чем можно убедиться, рассматривая их аналитические выражения:
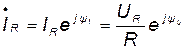 (8.1)
(8.1)
и 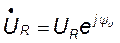 . (8.2)
. (8.2)
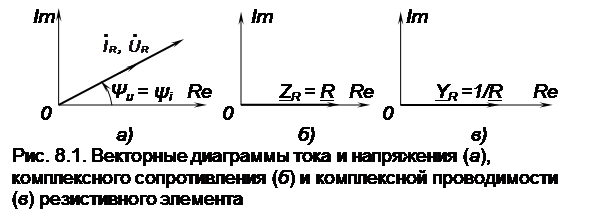
На комплексной плоскости напряжение и ток резистивного элемента изображаются векторами, которые совпадают по направлению и отличаются только масштабом (рис. 8.1, а)
 |
Комплексное сопротивление резистивного элемента в показательной и алгебраической формах имеет вид:
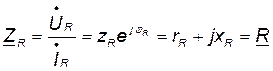 , (8.3)
, (8.3)
где 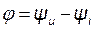 =0; хR = 0; rR = R.
=0; хR = 0; rR = R.
На комплексной плоскости (см. рис.8.1, б) сопротивление Z R изображается вектором, направленным вдоль вещественной оси.
Комплексная проводимость резистивного элемента (см. рис. 8.1, в) также изображается вектором, направленном вдоль вещественной оси
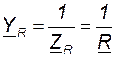 . (8.4)
. (8.4)
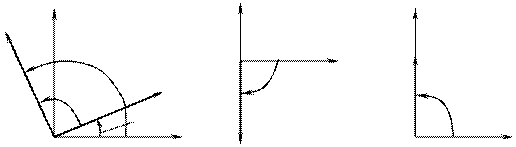
Комплексные ток и напряжение ёмкости изображаются на комплексной плоскости в виде двух векторов, расположенных таким образом, что вектор 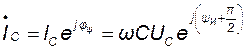 повернут относительно вектора
повернут относительно вектора 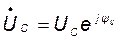 на угол
на угол 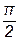 против хода часовой стрелки (рис. 8.2, а)
против хода часовой стрелки (рис. 8.2, а)
 |
|
Комплексные сопротивление и проводимость ёмкости:
 (8,5)
(8,5)
 (8.6)
(8.6)
Анализируя выражения (8.5) и (8.6) находим модули, аргументы, вещественные и мнимые составляющие комплексного сопротивления и комплексной проводимости ёмкости:
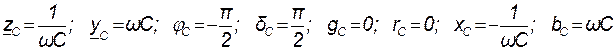 На комплексной плоскости комплексные числа Z C и Y C изображают векторами, направленными соответственно вдоль отрицательной или положительной мнимых полуосей (рис. 8.2 б, в).
На комплексной плоскости комплексные числа Z C и Y C изображают векторами, направленными соответственно вдоль отрицательной или положительной мнимых полуосей (рис. 8.2 б, в).
Комплексный ток и комплексное напряжение индуктивности определяются выражениями
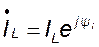 , (8.7)
, (8.7)
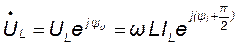 . (8.8)
. (8.8)
|
Используя выражения (8.7) и (8.8), находим комплексное сопротивление и комплексную проводимость индуктивности:
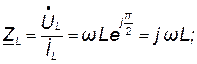 (8.9)
(8.9)
 (8.10)
(8.10)
Анализируя выражения (8.9) и (8.10), находим модули, аргументы, вещественные и мнимые составляющие комплексного сопротивления и комплексной проводимости индуктивности:
 (8.11)
(8.11)
где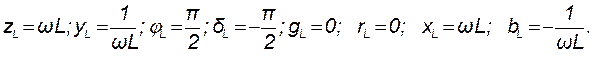
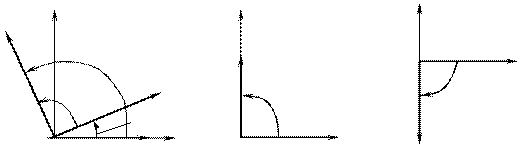
На комплексной плоскости комплексные числа Z L и Y L изображают векторами, направленными соответственно вдоль положительной или отрицательной мнимых полуосей (рис. 8.3, б, в)
Обобщением методов анализа R, L и С цепей при гармоническом воздействии является представление всех этих элементов цепи в виде комплексных сопротивлений (проводимостей) и использовании для их исследования законов постоянного тока.
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 369; Нарушение авторских прав?; Мы поможем в написании вашей работы!
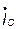 Ψi 0 Re YC=jωC=jbC
π/2
Ψi 0 Re YC=jωC=jbC
π/2 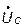 φ=─π/2
ψi δ=π/2
0 Re
φ=─π/2
ψi δ=π/2
0 Re  0 Re
a) б) в)
Рис. 8.2. Векторные диаграммы тока и напряжения (а), комплексного сопротивления (б) и комплексной проводимости (в) ёмкостного элемента
0 Re
a) б) в)
Рис. 8.2. Векторные диаграммы тока и напряжения (а), комплексного сопротивления (б) и комплексной проводимости (в) ёмкостного элемента
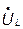 Ψu Z L=jωL=jxL 0 Re
Ψu Z L=jωL=jxL 0 Re
 δ=-π/2
π/2 φ=π/2
ψi Y L=-j/ωL=jbL
0 Re 0 Re
a) б) в)
Рис. 8.3 Векторные диаграммы тока и напряжения (а), комплексного сопротивления (б) и комплексной проводимости (в) индуктивного элемента
δ=-π/2
π/2 φ=π/2
ψi Y L=-j/ωL=jbL
0 Re 0 Re
a) б) в)
Рис. 8.3 Векторные диаграммы тока и напряжения (а), комплексного сопротивления (б) и комплексной проводимости (в) индуктивного элемента