Колебательного контура

Резонансная частота и добротность параллельного

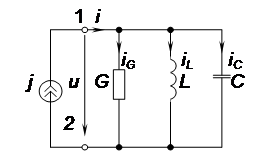
Схема параллельного колебательного контура изображена на рис. 11.2

		Рис. 11.2. Схема параллельного колебательного контура

Из анализа рис. 11.2 следует, что на резонансной частоте (ω = ω_P) мнимая составляющая входной проводимости параллельной RLC – цепи должна быть равна нулю:

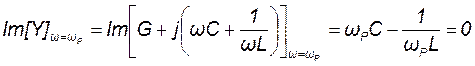. (11.9)

Решая уравнение (11.9), находим, что резонансная частота параллельного колебательного контура ω_Р совпадает с резонансной частотой последовательного контура ω₀, составленного из тех же элементов:

. (11.10)

На резонансной частоте проводимости ёмкости и индуктивности равны характеристической проводимости параллельного колебательного контура , которая является величиной, обратной характеристическому сопротивлению контура ρ.

При резонансе действующее значение тока ёмкости равно действующему значению тока индуктивности: 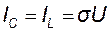, а входной ток контура равен току проводимости: .

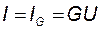На частоте резонанса токов ω = ω_Р сопротивление параллельного колебательного контура имеет чисто резистивный характер (φ = 0), а модуль сопротивления контура достигает максимального значения:

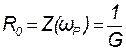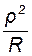=. (11.11)

На частотах ниже резонансное сопротивление параллельного контура имеет резистивно-индуктивный характер 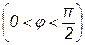, а на частотах выше резонансной – резистивно-емкостной .

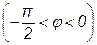Добротностью параллельного колебательного контура является отношение

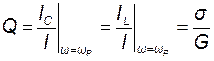. (11.12)

Из выражения (11.12) следует, что с увеличением проводимости потерь G добротность параллельного колебательного контура падает.

Характеристическое сопротивление параллельного контура, равное абсолютному значению мнимых составляющих сопротивлений ветвей контура на резонансной частоте, определяется тем же выражением, что и характеристическое сопротивление последовательного контура, а именно:

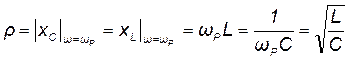. (11.13)

Ток i и напряжение u на зажимах 1-2 (см. рис. 11.2) на резонансной частоте совпадают по фазе, а их действующие значения

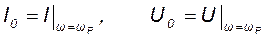
связаны между собой соотношением

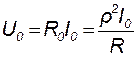. (11.14)

Используя выражение (11.14), находим добротность параллельного колебательного контура:

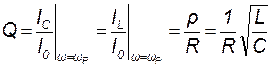. (11.15)

Из выражения (11.15) видно, что добротность параллельного колебательного контура совпадает с добротностью (11.8) последовательного колебательного контура, составленного из тех же элементов.

Рассмотрим частотные характеристики колебательных контуров, с помощью которых оценим избирательные (селективные) свойства этих колебательных контуров.

Дата добавления: 2014-01-15