Колебательного контура. Частотные характеристики последовательного

Частотные характеристики последовательного

X_C X_L I φ R Z Z X_L I R 90⁰ φ 0 ω 0 ω ω₀ ω₀ X_C -90⁰ а) б)

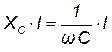Для получения частотных характеристик колебательного контура (рис. 11.1) к его зажимам 1-2 прикладывают переменное напряжение u, а в качестве отклика цепи рассматривают ток контура i, сдвиг фазы φ(ω) между этим током i в цепи и приложенным напряжением u, а также напряжение на ёмкости u_C = или напряжение на индуктивности u_L= в зависимости от частоты ω. Упомянутые частотные зависимости I(ω), φ(ω), Х_С (ω), Х_L (ω), а также R(ω) и Z(ω) изображены на рис. 11.3, а и б.

		Рис. 11.3. Частотные характеристики последовательного колебательного контура

Из рис. 11.3, а и б следует, что R(ω) = const – активное сопротивление контура;

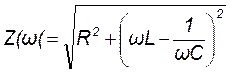- полное сопротивление колебательного контура, которое изменяется по закону параболы;

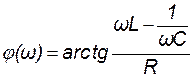- фазовый сдвиг между током I в цепи колебательного контура и приложенным напряжением u, который в момент резонанса равен нулю.

На практике находят широкое применение нормированные частотные характеристики. В качестве аргумента нормированных характеристик используют:

- абсолютную расстройку ;

- относительную расстройку ;

-нормированную частоту ;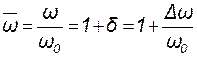

- обобщенную расстройку

,

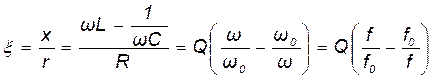где Q – добротность колебательного контура, указанная в выражении (11.8).

Зависимости падений напряжений на емкости u_C и индуктивности u_L последовательного колебательного контура от частоты представлены на рис. 11.4

Из рис. 11.4 следует, что амплитуды напряжений U_CMAX и U_MAX равны между собой и, кроме того, на резонансной частоте (ω = ω₀) имеет место равенство:

u_C = u_L =Q·U

Смещения максимумов U_CMAX и U_LMAX относительно резонансной частоты очень малы и на практике ими можно пренебречь.

Параллельный колебательный контур, подобно последовательному, обладает аналогичными частотными характеристиками.

Нормированные амплитудно-частотные и фазовые – частотные характеристики сопротивления параллельного колебательного контура совпадают с соответствующими нормированными характеристиками проводимости последовательного колебательного контура и выражаются зависимостями:

; (11.16)

. (11.17)

Все, что ранее говорилось о частотных характеристиках последовательного контура, справедливо и для частотных характеристик параллельного контура. В частности, при высокой добротности контура на частотах, близких к резонансной, имеет место

.

Дата добавления: 2014-01-15